ダメージ計算
目次 (ダメージ計算)
ダメージ計算
与ダメージ
①
[最終攻撃力]=[素攻撃力] * (1 + [限凸lv]/10 + ([特性] + [オプション] + [装備] + [AF] + [バフ※1] + [スキル※2] + [宝玉] + [食事lv])/ 100) + [スキル※3])
※1回復キャラが持つバフ
※2攻撃力upするスキル(ラムの青嵐のアルカナ等)
※3hpを攻撃力に変換するスキル(メアの第二人格)
②
[クリティカルダメージ]=[最終攻撃力]/2 * [スキル※4] /100* 1.5 * (1 +[限凸lv]/ 10 + ([オプションクリダメ] + [装備クリダメ])/100) - (敵防御 * (1 - [防御デバフ※4]/100))
※4メルルのスキル
③
[ノーマルダメージ]=[最終攻撃力]/2 * [スキル※5]/100 - (敵防御 * (1 - [防御デバフ※4]/100))
※4メルルのスキル
※5スキルのダメージ倍率(メアのパニックボム等)
与ダメージ計算サンプル
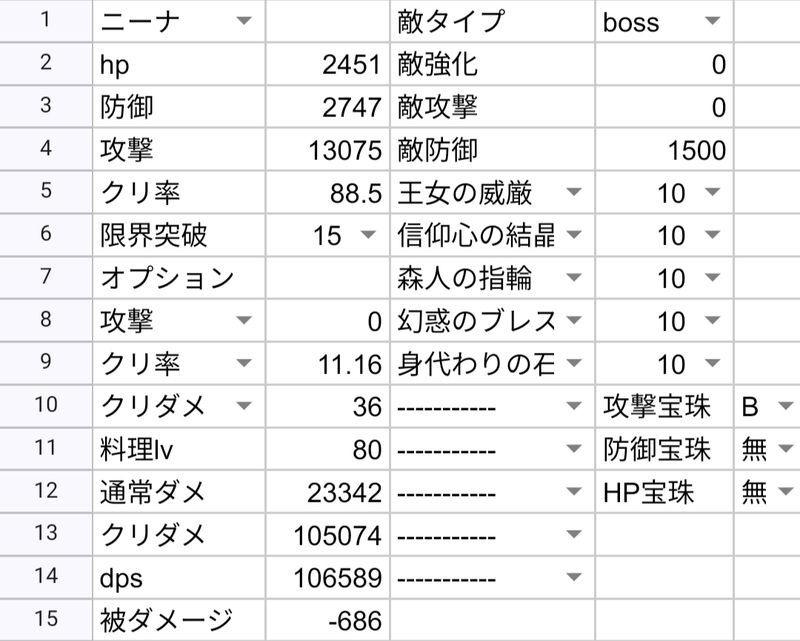
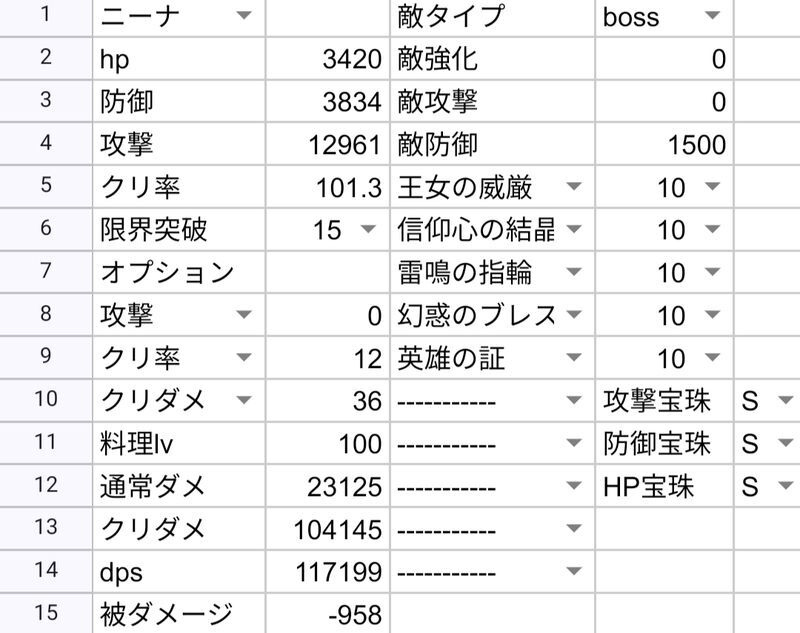
- 例 ニーナ

装備
AF(物理50後衛50)宝玉(攻撃S hpA 防御A)
・バフ込みのダメージを算出する為に素攻撃力の逆算
①より
[9307]=[素攻撃]* (1 + [15]/10 + ([80] + [120] + [0] + [100] + [0] + [115] + [150] + [0])/ 100) + [0])
素攻撃=1141.96...
小数点以下を四捨五入して素攻撃力は1142
・攻撃50%バフ込みの最終攻撃力の算出
①より
[最終攻撃力]=[1142] * (1 + [15]/10 + ([80] + [120] + [0] + [100] + [50] + [115] + [150] + [0])/ 100) + [0])
最終攻撃力=9878
・クリティカルダメージの算出
②より
[クリティカルダメージ]=[9307]/2 * [380] /100 * 1.5 * (1 +[15]/ 10 + ([16.92] + [46])/100) - (8750 * (1 - [0]/100)
クリティカルダメージ=74251
[クリティカルダメージ]=[9878]/2 * [380] /100 * 1.5 * (1 +[15]/ 10 + ([16.92] + [46])/100) - (8750 * (1 - [0]/100)
クリティカルダメージ=79344
実測値とほぼ一致
1の誤差は、恐らく素攻撃力の計算で四捨五入した為
・ノーマルダメージの算出
③より
[ノーマルダメージ]=[9307]/2 * [380]/100 - (8750 * (1 - [0]/100)
ノーマルダメージ=8933
[ノーマルダメージ]=[9878]/2 * [380]/100 - (8750 * (1 - [0]/100)
ノーマルダメージ=10018

防御デバフ
2025/6/5現在ではメルルのみ

最終攻撃力
バフ無21146バフ有21984
クリダメオプション35.28
バフ無
[197472]=[21146]/2 * [450] /100* 1.5 * (1 +[15]/ 10 + ([35.28] + [0])/100) - (8750 * (1 - [30]/100))
[41453]=[21146]/2 * [450]/100 - (8750 * (1 - [30]/100))
バフ有
[205541]=[21984]/2 * [450] /100* 1.5 * (1 +[15]/ 10 + ([35.28] + [0])/100) - (8750 * (1 - [30]/100))
被ダメージ
①
[ダメージ]=(([敵攻撃力] - [攻撃デバフ※1])/2*(1+[敵強化※2]/100*回数)*(1-[AF※3]/100)-[キャラ防御]/4)*(1-([オプ被ダメ減] + [装備被ダメ減])/100)
※1フィーのスキル
※2ボスの強化
裏400fボスの強化率を6.85%と仮定
強化時の全体攻撃はノイズとして処理
頻出するダメージを参照する。

強化0バフ無808有891


強化1バフ無1011有928

強化2バフ無1131有1049


強化3バフ無1251有1169
下記の数字は計算式より、ほぼ一致
※3グングニルの軽減率
被ダメージ計算サンプル
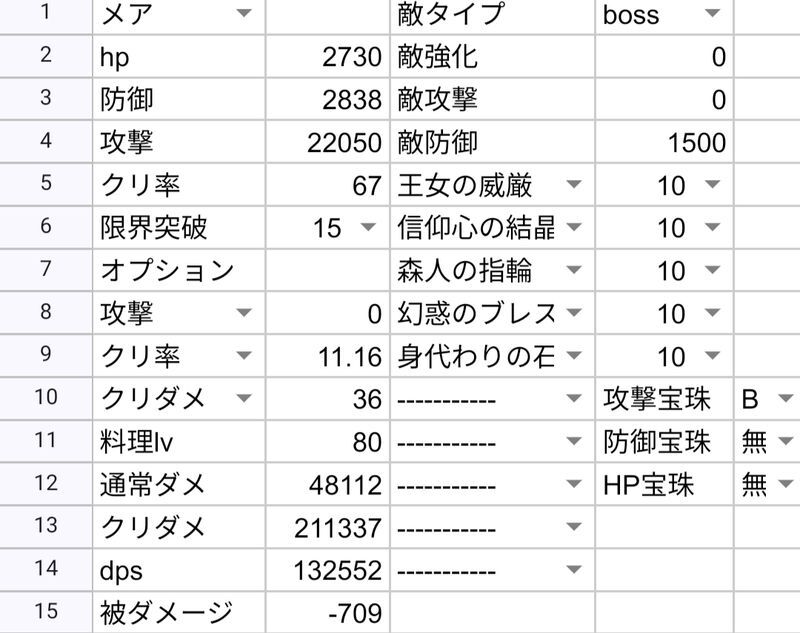
- 例 メア
a.
b.
aは戦闘開始時のログ(5桁のログから確認が出来る)
bはaから数秒後のログ
bの与ダメージに対してaの方が高い事からアイラのバフが確認出来る。
これよりaはバフ有3808でbはバフ無3478
敵攻撃力4400
①より
[ダメージ]=(([4400] - [0])/2*(1+[敵強化]/100*0)*(1-[20]/100)-[3808]/4)*(1-[0] + [0])/100)
ダメージ=808
[ダメージ]=(([4400] - [0])/2*(1+[敵強化]/100*0)*(1-[20]/100)-[3478]/4)*(1-[0] + [0])/100)
ダメージ=890
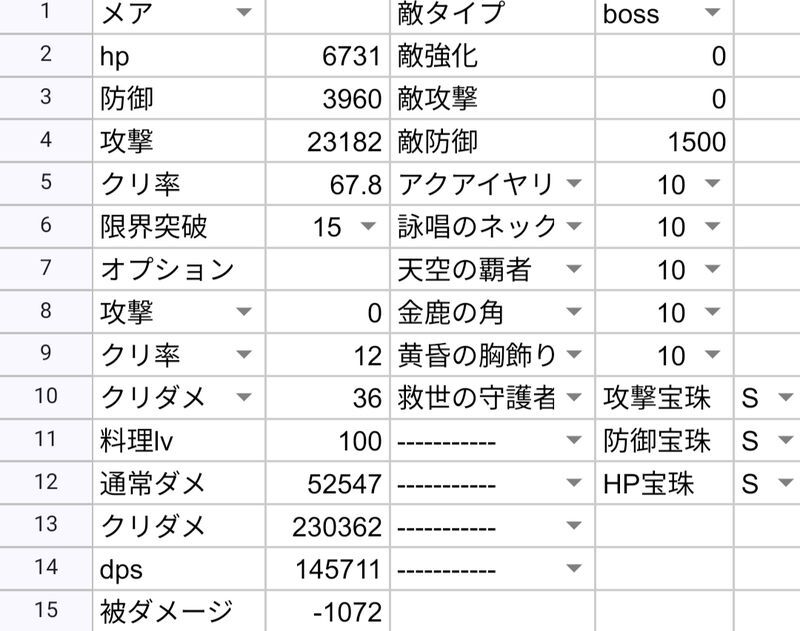
- 例 アイラ
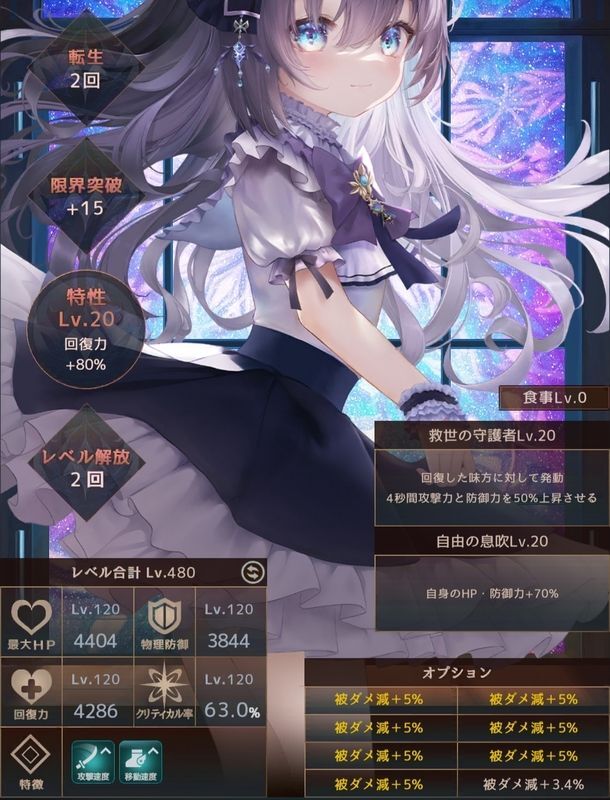
装備
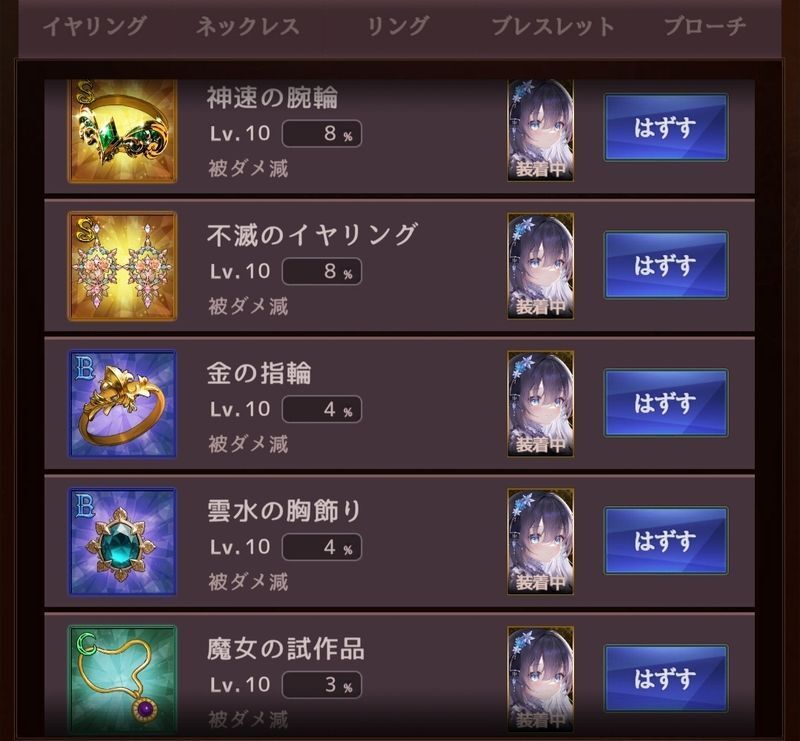
a.(宝玉B)
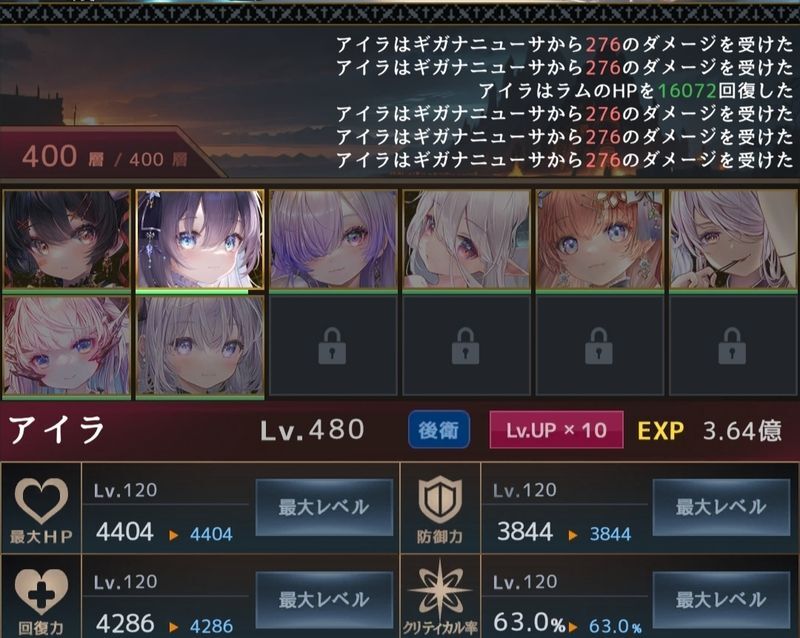
①より
[ダメージ]=(([4400] - [0])/2*(1+[敵強化]/100*0)*(1-[20]/100)-[3844]/4)*(1-[38.4] + [27])/100)
ダメージ=277
b.(宝玉S)
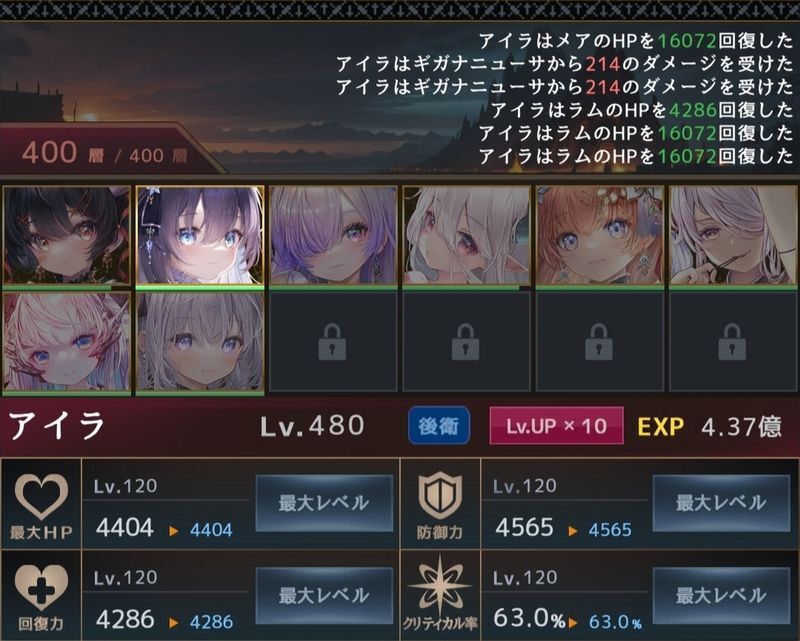
①より
[ダメージ]=(([4400] - [0])/2*(1+[敵強化]/100*0)*(1-[20]/100)-[4565]/4)*(1-[38.4] + [27])/100)
ダメージ=214
c.(宝玉B、攻撃デバフ)
[ダメージ]=(([4400] - [300])/2*(1+[敵強化]/100*0)*(1-[20]/100)-[3844]/4)*(1-[38.4] + [27])/100)
ダメージ=235
攻撃デバフvs防御バフ
これは殊座のハスキーハウリングの効果量と同じ
ハスキーハウリングの効果を消しフィーの臨機応変にすると770で、この時の比率が1.049...になる。
次に敵の攻撃を4400から1000000としてみると
ハスキーハウリングが39048で臨機応変が39010となり比率は1.00097...になり
更に敵の攻撃を10000000000にしてみると
ハスキーハウリングが3999999048で臨機応変が3999999010となり比率が1.00000001...なる。
つまり、敵の攻撃が高くなるほどフィーデバフの効果が小さくなるが、これ位の攻撃桁数では殊座よりフィーの方が強い。
ただし、これ以上桁数を上げても誤差なので他のメリット・デメリットを考えると
殊座は、防御の補正が低かったり複数体の敵の場合に有利だが、1000F以降の裏ステージになるとパーティー全体に効果が及ばない
フィーは、単体ならパーティー全体に効果を及ぼすが複数体だと効果が行き渡らない可能性がある。
防御vs被ダメージ減少
オプションで、防御と被ダメージ減少のどちらが有利かであるが
被ダメージは、式の後半で計算するので式の前半が大きい数でキャラ防御の影響が小さくなるほど効果が大きくなる。
例えば、ボスが強化を重ね攻撃が高くなったり、敵の素攻撃力が高い時などがそれに該当する。
例 メアが未強化の裏400fボスから受けるダメージが890
この時、オプションを防御240にすると受けるダメージが494になり被ダメ減40にすると534になる。
ここで敵の攻撃を4400から4700にすると、防御240は614で被ダメ減40が606で減少率が逆転する。
この辺りは補正で条件が変わるので、大雑把にゲームの序盤は防御が有利で、裏ステージ中層位から価値が逆転する位で良さそう。
Dps
[攻撃回数]=1/([攻撃速度※1]+[遅延※2])
※1 1回あたりの攻撃時間
※2 射程の短いキャラが敵の攻撃を受けると後退により遅延が発生する。
キャラクターが攻撃後に自発的に後退するものとは別物
射程の短いキャラで被ダメージを良く受けるポジションに置く場合は、敵の攻撃頻度から攻撃1回あたりの遅延時間を追加する。
攻撃を受け難いポジションで影響が少なそうなら無視
参考
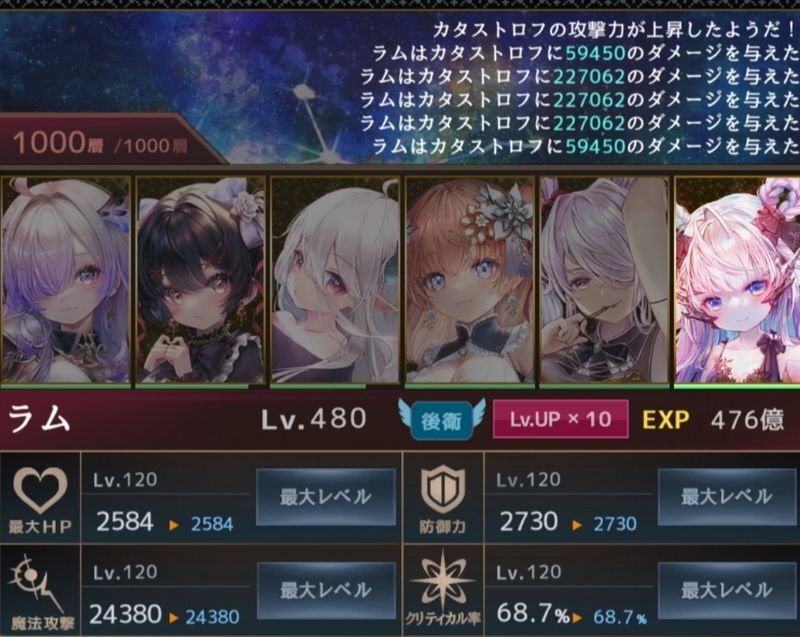
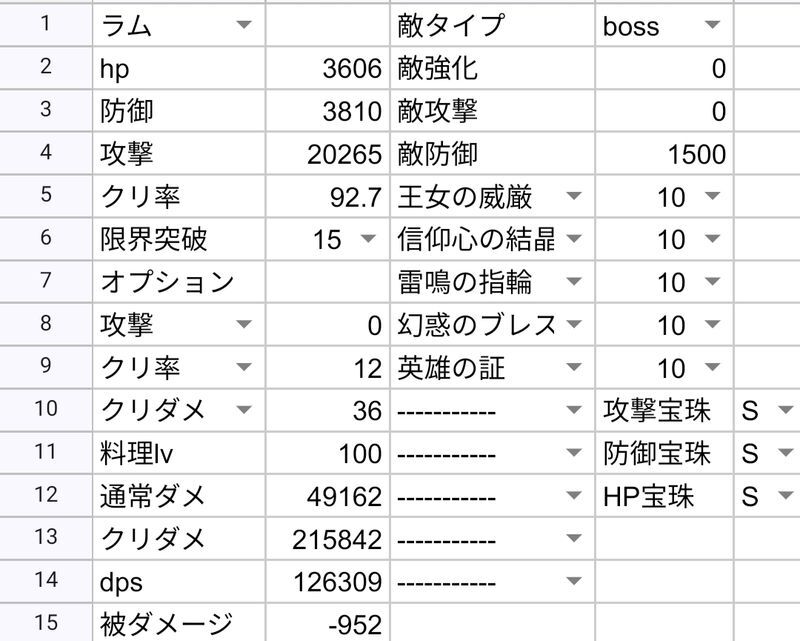
ラム1.6125
メア1.188
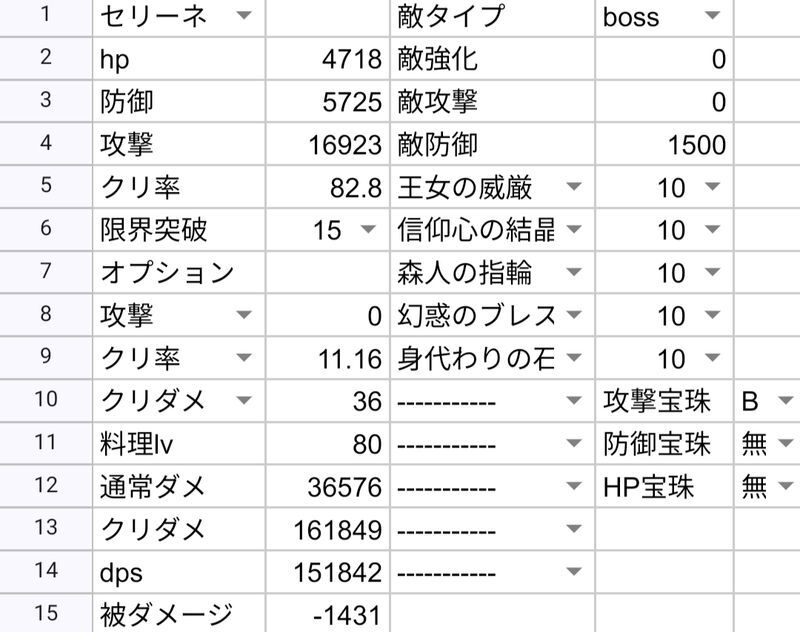
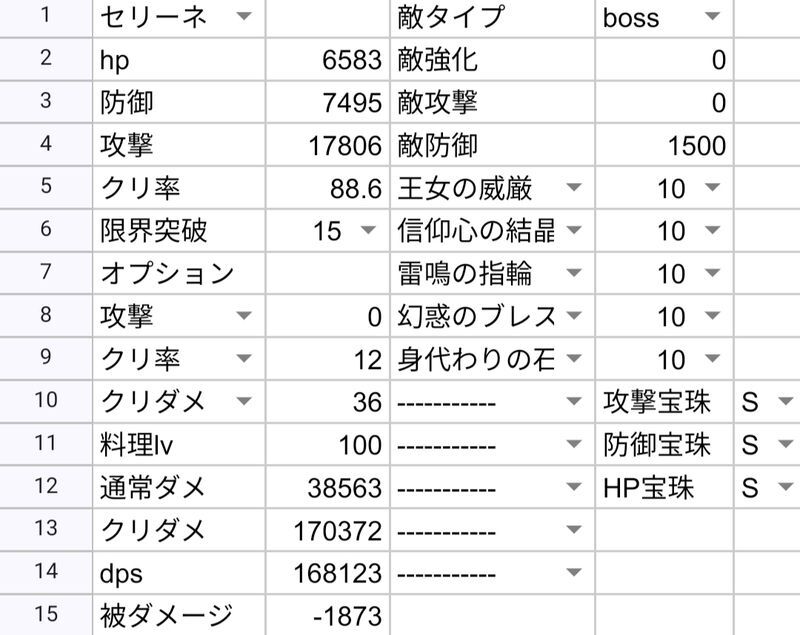
セリーネ0.924
ニーナ0.8976
[Dps]=(([クリティカルダメージ]-[ノーマルダメージ])*[クリティカル率]/100+[ノーマルダメージ])*[攻撃回数]
Dpsサンプル
| Dps1 | Dps2 | Dps3 | Dps4 | |
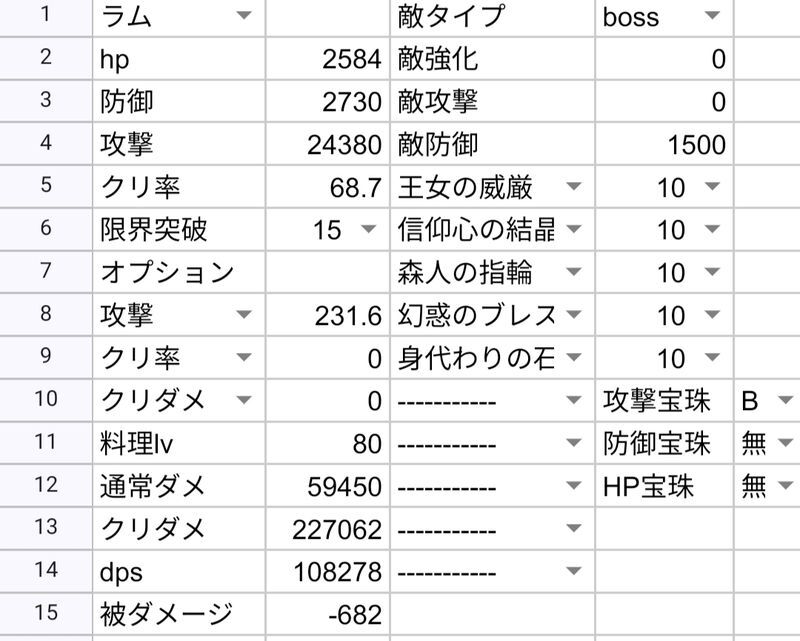
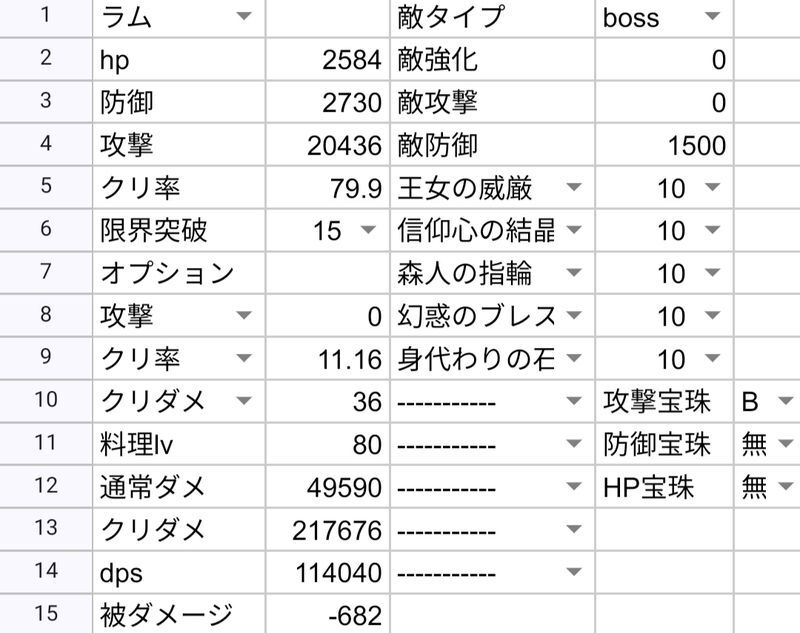
| ラム | 94736 | 108278 | 114040 | 126309 |
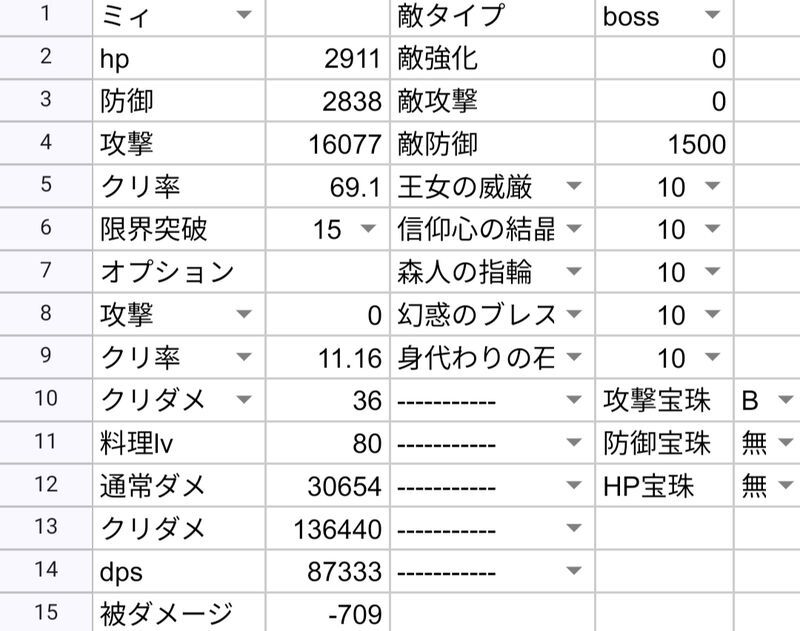
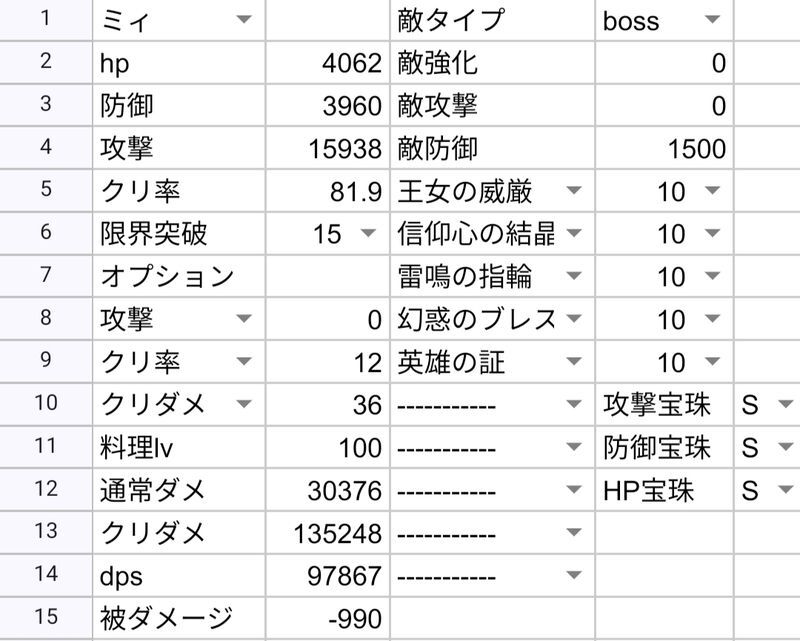
| ミィ | 87333 | 97867 | ||
| ニーナ | 106589 | 117199 | ||
| メア | 132552 | 145711 | ||
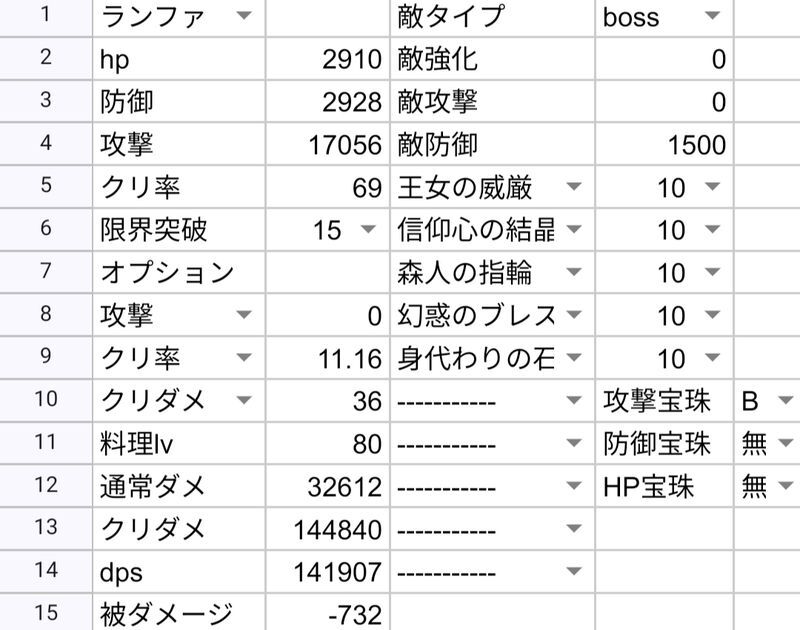
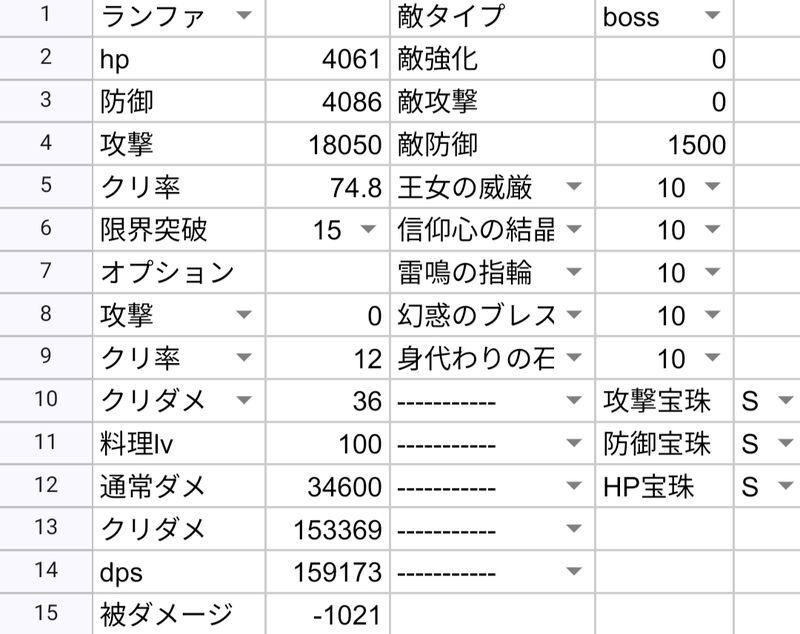
| ランファ | 141907 | 159173 | ||
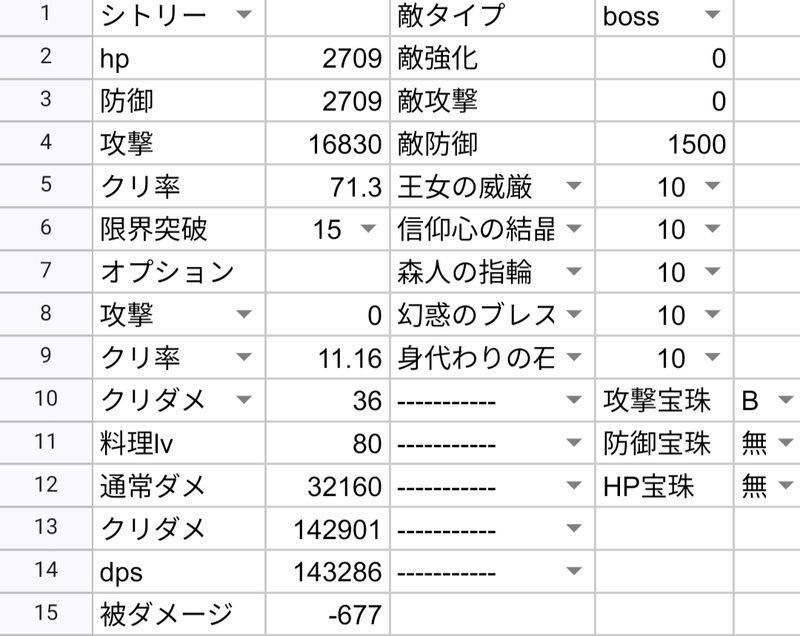
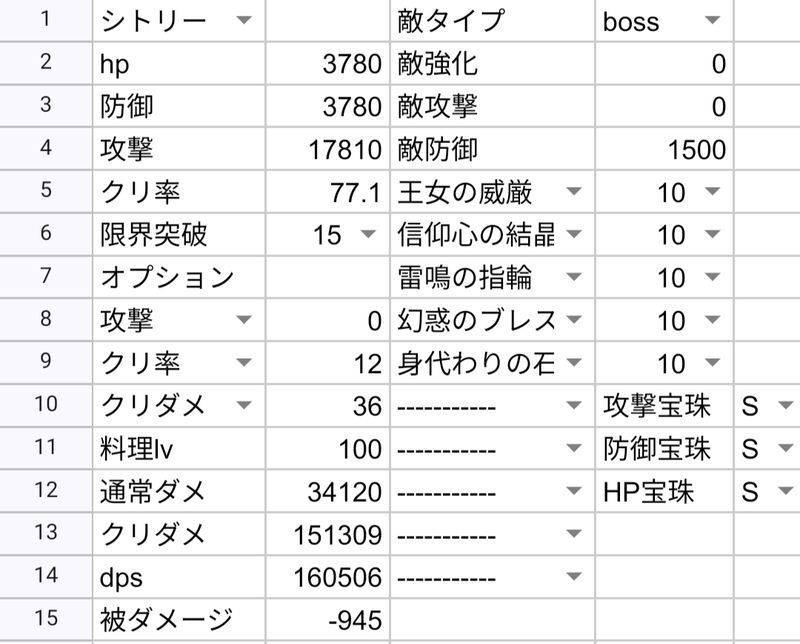
| シトリー | 143286 | 160506 | ||
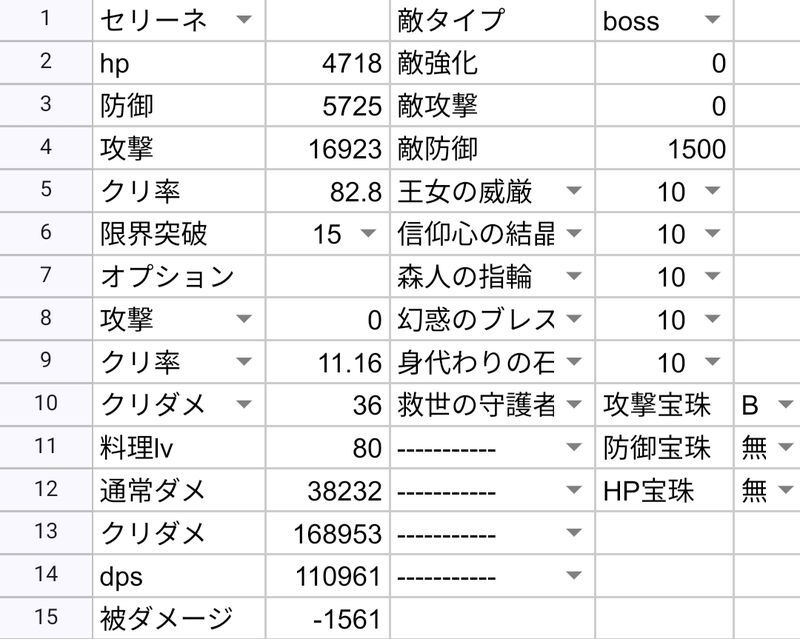
| セリーネ | 110961 | 151842 | 168123 |
防御デバフによるTotalDps
メルルデバフ(鎧通し)でどの程度TotalDpsが変わるのか
編成
装備
| メア | フィ | こあ | ラン | シト | セリ | ニー | |
| a | 89765 | 5114 | 16997 | 114493 | 84513 | 88088 | 75219 |
| a' | 91975 | 6835 | 20237 | 117877 | 87898 | 91473 | 78604 |
| A | 2210 | 1721 | 3240 | 3384 | 3385 | 3385 | 3385 |
| b | 91822 | 112871 | 72037 | 73094 | 58760 | ||
| b' | 94032 | 116256 | 75422 | 76479 | 62145 | ||
| B | 2210 | 1721 | 3240 | 3385 | 3385 | 3385 | 3385 |
| c | 123233 | 12738 | 27185 | 143609 | 115619 | 121662 | 89607 |
| c' | 125442 | 14654 | 31864 | 146994 | 119004 | 125047 | 92532 |
| C | 2209 | 1916 | 4679 | 3385 | 3385 | 3385 | 2925 |
| d | 134475 | 149824 | 111341 | 115283 | 87079 | ||
| d' | 136685 | 153209 | 114726 | 118668 | 90004 | ||
| D | 2210 | 1916 | 4679 | 3385 | 3385 | 3385 | 2925 |
| e | 129214 | 8639 | 20785 | 141765 | 103282 | 107224 | 80116 |
| e' | 133002 | 11590 | 24065 | 147568 | 109085 | 113027 | 85130 |
| E | 3788 | 2951 | 3280 | 5803 | 5803 | 5803 | 5014 |
a.攻撃240
b.クリ率12クリダメ36
c.攻撃240宝玉S料理100
d.クリ率12クリダメ36宝玉S料理100
a〜d.敵防御8750(裏400fボス)
e.クリ率12クリダメ36宝玉S料理100敵防御15000
x'.鎧通し
大文字=小文字'-小文字
| A | 20890 |
| B | 20711 |
| C | 21884 |
| D | 21885 |
| E | 32442 |
より、敵の防御が上がるほど鎧通しの価値が上がる。
また、ヒーラーは敵に攻撃をしないのでヒーラーの数が多いほど鎧通しの価値が下がり攻撃キャラが多いほど価値が上がる。
上記の編成の場合、空き枠が4つあり1枠をメルルとすると最大で3枠攻撃キャラに使用が出来る。
2転生未装備攻撃240宝玉・料理無しラムが防御8750の敵に対してDpsが58652、宝玉S料理100で77721で鎧通しでDpsが1621上がる。
他の2キャラもこれと同等と考えると回復1の12編成でTDps26000上がり
敵防御15000の時は、鎧通しで2790のTDpsが41000上がる。
敵防御が8750程度では攻撃キャラの装備の都合がつかなくても素直に攻撃キャラを入れた方がTDpsは高い。
ただし、表1000のボス防御が1500でそれから比べるとかなり上昇しているのと編成全体の安定性を考えた時に自身の耐久を上げかつ火力上昇が見込めるメルルは将来的には面白い存在になりそう。
オプション
素の攻撃が100として、補正50のaと補正100のbがある。
これに補正を50を加えた時の上昇率を考える。
最終攻撃力は
素攻撃*(1+補正値/100)で
a.100*(1+(50+50)/100)=200
b.100*(1+(100+50)/100)=250
50補正を加える前のaが150でbが200で、上昇率はaが0.25でbが0.2となる。
つまり、同じ補正を加えたとしても元の補正により1辺りの価値が変わる。
ダメージ式を簡略化すると攻撃・クリティカル率・ダメージはA*B*Cの関係にあり、ダメージの最大化はこの比率による。
ラムやニーナの様にスキルに補正を持ち攻撃補正の価値が下がる場合や、メアの様なhpを攻撃として最終攻撃力が高くなるときクリティカル率・ダメージの価値が上がる。
ただその場合でも補正の合計が500〜700位だった筈だから、攻撃偏重の装備だったり宝玉・料理等の設備投資が終わり攻撃を上げやすい状況でなければオプションは攻撃で良い。
限界突破・転生
| ランファ | 未転生 | 転生1 | 転生2 |
| 限凸10 | 23128 | 25603 | 28077 |
| 限凸11 | 25280 | 27914 | 30555 |
| 限凸12 | 27496 | 30302 | 30555 |
| 限凸13 | 29777 | 32756 | 35728 |
| 限凸14 | 32122 | 35272 | 38428 |
| 限凸15 | 34531 | 37864 | 41196 |
補正AF100装備120料理30,攻撃(1439,1547.5,1656)
| ランファ | 未転生 | 転生1 | 転生2 |
| 限凸10 | 32731 | 35928 | 39125 |
| 限凸11 | 35269 | 38658 | 42047 |
| 限凸12 | 37871 | 41458 | 45044 |
| 限凸13 | 40538 | 44327 | 48109 |
| 限凸14 | 43269 | 47259 | 51253 |
| 限凸15 | 46065 | 50265 | 54466 |
補正AF100装備120料理30宝玉150
攻撃(1439,1547.5,1656)
限凸・転生1あたり8%Dpsが上昇
転生1を転生2にして同じ水準までの必要経験値が約9億
そこから攻撃とクリを120まで必要経験値が約14億
ランファとシトリーの凸を10から11にした時(シトリーはランファとほぼ同じスペックなのでランファとする)
宝玉150ランファ10→11で2538、宝玉無しシトリー10→11で2152になり上昇量は4690
宝玉150ランファを10→12にした時の上昇量が5140
限凸素材が多少増えるから単純比較が出来ないが
後者の方が高い。
また、シトリーよりDpsが低い場合、上昇率が同じでも上昇元が下がれば上昇量も減るので上昇元が高い高Dpsのキャラに装備等を集中して限凸するのが恐らく効率が良い。
Hps
単体のhps
(回復力*(1+限凸lv/10)*1.5*クリ率/100+回復力*(1-クリ率)/100)/攻撃速度
また、ナツナの追加回復は
(回復力*0.3*(1+限凸lv/10)*1.5*クリ率/100+回復力*0.3*(1-クリ率)/100)/攻撃速度
実際はHP上限があるので、
回復力*(1+限凸lv/10)*1.5*クリ率/100が
上限値に届く場合それを上限とする。
| 回復力4500/HP上限5000 ()内はナツナの追加回復 | |||
| クリ率/攻速 | 50% | 80% | 100% |
| 0.9 | 5278 | 5444 | 5556 |
| 1 | 4750 | 4900 | 5000 |
| 1.5 | 3167 | 3267 | 3333 |
| 2 | 2375(1587) | 2450(2135) | 2500(2500) |
上限を5000とした時、ナツナのクリ率が100%だと
実質5人に回復力100%で回復になる。
また、
3000/0.56=5357
回復が範囲の場合はこれに人数条件を加える。
-
-

-
ななしの投稿者
-
-
-

-
 ななしの投稿者
ななしの投稿者
42カ月まえ ID:f1d25rvj自分用で必要な箇所以外はとっ散らかっているので公開するつもりは無いです。計算自体は簡単なので、計算結果が実測値に収まらないのであれば、補正が少ない又は無いキャラで計算を簡素にして合致する部分から徐々に肉付けして行けば形になるかと思います。1から15行に収まらないと言う意味であれば複数のシートにキャラやスキル等をdb化してそこから情報を持ってきていたりするので、15行のスペースには収まらないです
-
-
-

-
ななしの投稿者
32カ月まえ ID:bm1tbmzuユーザー97335様、編集ありがとうございます。
自分も計算して編成を見直していますが、なかなかきれいに収まりません。こちらの記事で使われている1-15行の計算シートですが、公開などはされておりますでしょうか。ご教示いただけますと大変助かります<(_ _)>
-
-
-

-
ななしの投稿者
-
-
-

-
ななしの投稿者
17カ月まえ ID:f1d25rvj公式の情報じゃないので間違っている可能性あり。
5ch眺めてたらこっちでの自分の書き込み内容があってそれについてのちょっと説明する感じで書いてみた、みてる
-