排出率の推定
ガチャの確率に戻る
目次
★4排出率の推定
★4排出率を推定することを、統計学的には母比率の推定と呼びます。
前提として、ガチャ回数が十分に多く(100回以上)、出現した★4の回数が十分に多い(6回以上)とします。
出現した★4の回数をガチャ回数で割ったものをRと言うことにします。
R=(出現した★4の回数)÷(ガチャ回数)
です。Rは単純な★4排出率の推定値となります。
また、ガチャ回数もnという文字に置き換えておきます。
n=(ガチャ回数)
です。
あるdという値があるとします。
このdとRを使って
「★4排出率が(R-d)~(R+d)の間にある確率は95%である。」
と言いたいとします。
このときのdは多くの統計書に載っていて、次の式で表されます。
d=1.96√(R(1-R)/n)
Excel上では、dは次のように表すことができます。
=CONFIDENCE.NORM(0.05,SQRT(R*(1-R)),n)
例:ガチャを200回回して★4が17回出現した場合
R=17÷200=0.085
であるからExcelに
=CONFIDENCE.NORM(0.05,SQRT(0.085*(1-0.085)),200)
を入力すると、0.03865が得られる
範囲の下限は
0.085-0.03865=0.04635
範囲の上限は
0.085+0.03865=0.12365
以上より
「★4排出率が4.6%~12.4%の間にある確率は95%である」
ということがわかる
例の場合では95%を信頼度と呼び、4.6%~12.4%を信頼区間と呼びます。
この言葉を使って
「★4排出率の信頼度95%の信頼区間は4.6%~12.4%である」
と言うこともできます。
排出率の推定値がが10%だったとき、信頼区間は下のグラフのようにガチャ回数が増えるに連れて狭まっていきます。
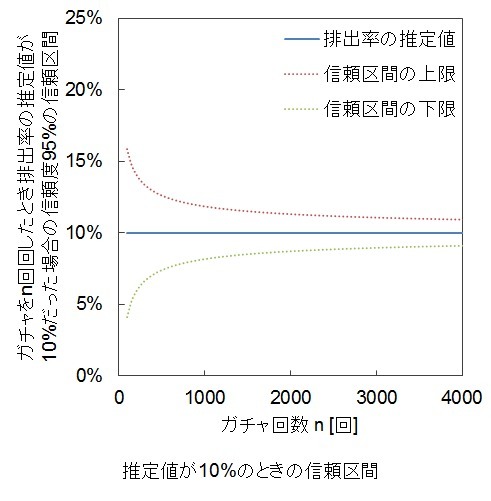
100回ガチャを回したときの信頼区間
| 出現した ★4の回数 | ★4排出率の 推定値 [%] | ★4排出率の 信頼度 95%の 信頼区間 [%] |
|---|---|---|
| 6 | 6.0 | 1.3~10.7 |
| 7 | 7.0 | 1.9~12.1 |
| 8 | 8.0 | 2.6~13.4 |
| 9 | 9.0 | 3.3~14.7 |
| 10 | 10.0 | 4.1~15.9 |
| 11 | 11.0 | 4.8~17.2 |
| 12 | 12.0 | 5.6~18.4 |
| 13 | 13.0 | 6.4~19.6 |
| 14 | 14.0 | 7.1~20.9 |
| 15 | 15.0 | 8.0~22.0 |
| 16 | 16.0 | 8.8~23.2 |
| 17 | 17.0 | 9.6~24.4 |
500回ガチャを回したときの信頼区間
| 出現した ★4の回数 | ★4排出率の 推定値 [%] | ★4排出率の 信頼度 95%の 信頼区間 [%] |
|---|---|---|
| 10 | 2.0 | 0.7~3.3 |
| 15 | 3.0 | 1.5~4.5 |
| 20 | 4.0 | 2.2~5.8 |
| 25 | 5.0 | 3.0~7.0 |
| 30 | 6.0 | 3.9~8.1 |
| 35 | 7.0 | 4.7~9.3 |
| 40 | 8.0 | 5.6~10.4 |
| 45 | 9.0 | 6.4~11.6 |
| 50 | 10.0 | 7.3~12.7 |
| 55 | 11.0 | 8.2~13.8 |
| 60 | 12.0 | 9.1~14.9 |
| 65 | 13.0 | 10.0~16.0 |
グラフで表すと下のようになります。
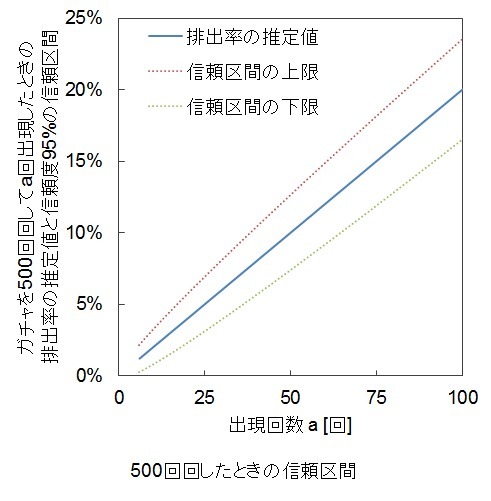
キャラガチャ合算2011回による検証値
この検証によりキャラガチャにおいて次の結論が得られました。
★2排出率の推定値は
50.1%
★2排出率の信頼度95%の信頼区間は
47.8%~52.3%
★3排出率の推定値は
40.1%
★3排出率の信頼度95%の信頼区間は
37.9%~42.3%
★4排出率の推定値は
9.8%
★4排出率の信頼度95%の信頼区間は
8.4%~11.1%
ここの排出率推定の結果はこのページにある「2015年8月31日 キャラガチャ641連」と「2016年1月29日 キャラガチャ913連」と「2016年2月29日 キャラガチャ457連」のデータを合算して検証したものです。
| ガチャ回数等 | |
|---|---|
| ガチャ回数 | 2011回 |
| 単発ガチャ回数 | 9回 |
| 「10回+1ガチャ」の回数 | 182回 |
| 消費ジュエル数 | 4万5725個 |
| iOSでの最安値 | 68万5875円 |
| Androidでの最安値 | 74万745円 |
| ★2 | ★3 | ★4 | |
|---|---|---|---|
| 出現回数 [回] | 1007 | 807 | 197 |
| 出現比率 [%] | 50.1 | 40.1 | 9.8 |
| d [%] | 2.2 | 2.1 | 1.3 |
| 信頼度95%の 信頼区間 [%] | 47.8~52.3 | 37.9~42.3 | 8.4~11.1 |
2015年8月31日 キャラガチャ641連による検証値
検証動画 You Tube へのリンク
https://www.youtube.com/watch?v=zD4m_fkMPxs
| ジュエルの チャージ時刻 | 出現回数 | 備考 | ||
|---|---|---|---|---|
| ★2 | ★3 | ★4 | ||
| 5 | 3 | 3 | オウガ×2 | |
| 5 | 4 | 2 | ||
| 4 | 7 | 0 | ||
| 3 | 8 | 0 | ||
| 7 | 4 | 0 | ||
| 7 | 4 | 0 | ||
| 5 | 6 | 0 | ||
| 2 | 5 | 4 | ||
| 8 | 2 | 1 | ||
| 5 | 5 | 1 | ||
| 3:38 | 5 | 6 | 0 | |
| 9 | 2 | 0 | ||
| 8 | 2 | 1 | ||
| 5 | 5 | 1 | ||
| 6 | 4 | 1 | ||
| 6 | 3 | 2 | ||
| 3 | 8 | 0 | ||
| 4 | 5 | 2 | ||
| 5:19 | 5 | 6 | 0 | |
| 5 | 3 | 3 | ||
| 8 | 3 | 0 | ||
| 7 | 3 | 1 | ||
| 4 | 6 | 1 | ||
| 6 | 5 | 0 | ||
| 3 | 6 | 2 | オウガ×2 | |
| 5 | 6 | 0 | ||
| 7:28 | 4 | 7 | 0 | |
| 8 | 1 | 2 | ||
| 7 | 4 | 0 | ||
| 5 | 5 | 1 | ||
| 2 | 6 | 3 | ||
| 5 | 3 | 3 | オウガ | |
| 6 | 4 | 1 | オウガ | |
| 5 | 3 | 3 | オウガ | |
| 5 | 6 | 0 | ||
| 7 | 4 | 0 | ||
| 10:23 | 6 | 4 | 1 | |
| 9 | 2 | 0 | ||
| 7 | 4 | 0 | ||
| 9 | 1 | 1 | ||
| 7 | 4 | 0 | ||
| 4 | 4 | 3 | オウガ | |
| 2 | 7 | 2 | ||
| 3 | 5 | 3 | ||
| 7 | 4 | 0 | ||
| 5 | 4 | 2 | ||
| 12:19 | 3 | 7 | 1 | |
| 6 | 4 | 1 | ||
| 7 | 3 | 1 | ||
| 5 | 5 | 1 | ||
| 7 | 4 | 0 | ||
| 7 | 2 | 2 | ||
| 5 | 4 | 2 | ||
| 2 | 1 | 0 | 単発×3 | |
| 14:20 | 5 | 4 | 2 | オウガ |
| 4 | 7 | 0 | ||
| 3 | 7 | 1 | ||
| 7 | 3 | 1 | ||
| 6 | 4 | 1 | シャルロット | |
| 合計 | 320 | 258 | 63 | |
検証結果
| ガチャ回数等 | |
|---|---|
| ガチャ回数 | 641回 |
| 単発ガチャ回数 | 3回 |
| 「10回+1ガチャ」の回数 | 58回 |
| 消費ジュエル数 | 1万4575個 |
| iOSでの最安値 | 21万8625円 |
| Androidでの最安値 | 23万6115円 |
| ★2 | ★3 | ★4 | オウガ+ シャルロット | オウガ | シャルロット | |
|---|---|---|---|---|---|---|
| 出現回数 [回] | 320 | 258 | 63 | 10 | 9 | 1 |
| 出現比率 [%] | 49.9 | 40.2 | 9.8 | 1.6 | 1.4 | 0.16 |
| d [%] | 3.9 | 3.8 | 2.3 | 1.0 | 0.9 | ※注 |
| 信頼度95%の 信頼区間 [%] | 46~53.8 | 36.4~44.1 | 7.5~12.2 | 0.6~2.6 | 0.4~2.4 |
※注 出現回数が少なすぎるためこの方法では検証できません
以下参考(小ネタ)
資金の溶解速度(iOSでの最安値、動画の再生時間を基準にしています)
78万円/時
| 各キャラクターの 出現比率から推定される★4排出率 | |
|---|---|
| オウガ+ シャルロット | 10.9% |
| オウガ | 19.7% |
| シャルロット | 2.2% |
以下では★4排出率を検証値(=63/641)と仮定し、ガチャに★4が14種類あるとします。
| ガチャを641回回して ★4の1点狙いをするとき | |
|---|---|
| ガチャ1回の成功確率 | 0.70% |
| 1点狙いが失敗する確率 | 1.1% |
| 1点狙いが成功する確率 | 98.9% |
| 狙っている★4の出現回数が 1回以下である確率 | 6.0% |
| 狙っている★4の出現回数が 9回以上である確率 | 4.0% |
| 狙っている★4が 出現する回数の期待値 | 4.5回 |
下の図で、赤い部分は動画投稿者が出したシャーロットの数1回以下となる確率、
青い部分は動画投稿者が出したオウガの数9回以上となる確率です。
| ★4の1点狙いが成功するまで ガチャを回すときの期待値 | |
|---|---|
| ガチャ回数 | 142回 |
| 消費ジュエル数 (10回+1ガチャ) | 3227個 |
| iOSでの最安値 | 4万8409円 |
「10回+1ガチャ」を58回ガチャったとき、「10回+1ガチャ」1回に特定の1種類の★4が2回以上出現する事象が2回以上起こる確率
1.0%
動画投稿者は再生時刻 1:14 のオウガが2回出現した場面にて
「ちなみに、僕オウガもう2回出ているんですよね。」
と言っています。
2016年1月29日 キャラガチャ913連による検証値
検証動画 You Tube へのリンク
https://www.youtube.com/watch?v=DrDbBhv8i2s
| 時刻 | 出現回数 | 備考 | ||
|---|---|---|---|---|
| ★2 | ★3 | ★4 | ||
| 7 | 3 | 1 | ||
| 5 | 4 | 2 | ||
| 2 | 6 | 3 | ||
| 7 | 3 | 1 | ||
| 4 | 5 | 2 | ||
| 5 | 5 | 1 | ||
| 6 | 3 | 2 | ||
| 8 | 2 | 1 | ||
| 6:20 | 7 | 2 | 2 | アーモンドプレミオ |
| 4 | 6 | 1 | ||
| 3 | 7 | 1 | ||
| 6 | 4 | 1 | アーモンドプレミオ | |
| 8 | 3 | 0 | ||
| 10:00 | 7 | 3 | 1 | |
| 8 | 0 | 3 | ||
| 7 | 2 | 2 | アーモンドプレミオ | |
| 6 | 5 | 0 | ||
| 7 | 3 | 1 | ||
| 6 | 5 | 0 | ||
| 4 | 5 | 2 | ||
| 3 | 6 | 2 | アーモンドプレミオ | |
| 4 | 7 | 0 | ||
| 5 | 6 | 0 | ||
| 8 | 3 | 0 | ||
| 6 | 5 | 0 | ||
| 5 | 6 | 0 | ||
| 7 | 1 | 3 | ||
| 15:00 | 4 | 6 | 1 | |
| 7 | 4 | 0 | ||
| 6 | 4 | 1 | ||
| 3 | 5 | 3 | ||
| 4 | 6 | 1 | ||
| 6 | 4 | 1 | ||
| 5 | 4 | 2 | ||
| 5 | 4 | 2 | ||
| 6 | 4 | 1 | アーモンドプレミオ | |
| 5 | 4 | 2 | ||
| 5 | 4 | 2 | ||
| 7 | 4 | 0 | ||
| 4 | 6 | 1 | ||
| 5 | 4 | 2 | アーモンドプレミオ | |
| 7 | 2 | 2 | ||
| 8 | 2 | 1 | ||
| 18:25 | 0 | 11 | 0 | 全部★3 |
| 5 | 5 | 1 | ||
| 4 | 6 | 1 | ||
| 9 | 2 | 0 | ||
| 7 | 3 | 1 | ||
| 20:03 | 3 | 6 | 2 | |
| 5 | 6 | 0 | ||
| 7 | 4 | 0 | ||
| 7 | 2 | 2 | ||
| 8 | 2 | 1 | ||
| 4 | 6 | 1 | ||
| 8 | 3 | 0 | ||
| 9 | 2 | 0 | ||
| 8 | 3 | 0 | ||
| 3 | 5 | 3 | ||
| 8 | 3 | 0 | ||
| 6 | 5 | 0 | ||
| 4 | 6 | 1 | ||
| 5 | 4 | 2 | ||
| 7 | 3 | 1 | ||
| 3 | 8 | 0 | ||
| 6 | 5 | 0 | ||
| 4 | 6 | 1 | ||
| 5 | 4 | 2 | ||
| 4 | 6 | 1 | ||
| 5 | 6 | 0 | ||
| 5 | 5 | 1 | ||
| 5 | 6 | 0 | ||
| 5 | 5 | 1 | ||
| 5 | 5 | 1 | ||
| 6 | 5 | 0 | ||
| 2 | 8 | 1 | ||
| 8 | 1 | 2 | ||
| 6 | 4 | 1 | ||
| 25:13 | 7 | 4 | 0 | |
| 3 | 7 | 1 | ||
| 7 | 3 | 1 | ||
| 6 | 4 | 1 | ||
| 5 | 4 | 2 | ||
| 25:48 | 6 | 4 | 1 | アーモンドピーク |
| 合計 | 462 | 364 | 87 | |
検証結果
| ガチャ回数等 | |
|---|---|
| ガチャ回数 | 913回 |
| 単発ガチャ回数 | 0回 |
| 「10回+1ガチャ」の回数 | 83回 |
| 消費ジュエル数 | 2万750個 |
| iOSでの最安値 | 31万1250円 |
| Androidでの最安値 | 33万6150円 |
| ★2 | ★3 | ★4 | アーモンドプレミオ+ アーモンドピーク | アーモンドプレミオ | アーモンドピーク | |
|---|---|---|---|---|---|---|
| 出現回数 [回] | 462 | 364 | 87 | 7 | 6 | 1 |
| 出現比率 [%] | 50.6 | 39.9 | 9.5 | 0.8 | 0.7 | 0.11 |
| d [%] | 3.2 | 3.2 | 1.9 | 0.6 | 0.5 | ※注 |
| 信頼度95%の 信頼区間 [%] | 47.3~53.9 | 36.6~43.1 | 7.6~11.5 | 0.2~1.4 | 0.1~1.2 |
※注 出現回数が少なすぎるためこの方法では検証できません
以下参考(小ネタ)
資金の溶解速度(iOSでの最安値、動画の再生時間を基準にしています)
70万円/時
最高瞬間溶解速度(22:20頃、6秒間に250個、3750円)
225万円/時
| 各キャラクターの 出現比率から推定される★4排出率 | |
|---|---|
| アーモンドプレミオ+ アーモンドピーク | 6.1% |
| アーモンドプレミオ | 10.5% |
| アーモンドピーク | 1.8% |
以下では★4排出率を検証値(=87/913)と仮定し、ガチャに★4が16種類あるとします。
| ガチャを913回回して ★4の1点狙いをするとき | |
|---|---|
| ガチャ1回の成功確率 | 0.60% |
| 1点狙いが失敗する確率 | 0.43% |
| 1点狙いが成功する確率 | 99.6% |
| 狙っている★4の出現回数が 1回以下である確率 | 2.8% |
| 狙っている★4の出現回数が 6回以上である確率 | 46.1% |
| 狙っている★4が 出現する回数の期待値 | 5.4回 |
| ★4の1点狙いが成功するまで ガチャを回すときの期待値 | |
|---|---|
| ガチャ回数 | 168回 |
| 消費ジュエル数 (10回+1ガチャ) | 3818個 |
| iOSでの最安値 | 5万7272円 |
次のものは★3排出率を検証値(=364/913)と仮定しています。
「10回+1ガチャ」を83回ガチャったとき、「10回+1ガチャ」1回で出現するキャラのすべてが★3となる事象が1回以上起こる確率
0.34%
2016年2月29日 キャラガチャ457連による検証値
検証動画 You Tube へのリンク
https://www.youtube.com/watch?v=o2iLha2NF54
| 時刻 | 出現回数 | 備考 | ||
|---|---|---|---|---|
| ★2 | ★3 | ★4 | ||
| 8 | 3 | 0 | ||
| 8 | 3 | 0 | ||
| 6 | 4 | 1 | ||
| 4 | 7 | 0 | ||
| 5 | 6 | 0 | 同じ★3キャラ3連続 | |
| 5:23 | 5 | 3 | 3 | 同じ★2キャラ3連続 |
| 4 | 5 | 2 | リンデ | |
| 5 | 5 | 1 | 同じ★2キャラ3連続 | |
| 4 | 7 | 0 | ||
| 4 | 5 | 2 | ||
| 4 | 7 | 0 | ||
| 10:05 | 4 | 6 | 1 | |
| 5 | 5 | 1 | ||
| 6 | 3 | 2 | ||
| 8 | 3 | 0 | ||
| 6 | 5 | 0 | ||
| 7 | 4 | 0 | ||
| 5 | 5 | 1 | ||
| 4 | 5 | 2 | リンデ | |
| 3 | 3 | 5 | ||
| 3 | 6 | 2 | ||
| 15:13 | 4 | 5 | 2 | リンデ |
| 5 | 5 | 1 | ||
| 6 | 4 | 1 | ||
| 4 | 6 | 1 | ||
| 5 | 4 | 2 | ||
| 5 | 6 | 0 | ||
| 5 | 5 | 1 | ||
| 8 | 3 | 0 | ||
| 17:30 | 5 | 5 | 1 | リンデ |
| 8 | 2 | 1 | ||
| 6 | 3 | 2 | ||
| 8 | 3 | 0 | ||
| 4 | 5 | 2 | リンデ | |
| 3 | 4 | 4 | ||
| 5 | 5 | 1 | ||
| 20:29 | 8 | 2 | 1 | |
| 5 | 5 | 1 | ||
| 8 | 3 | 0 | ||
| 7 | 3 | 1 | ||
| 6 | 3 | 2 | ||
| 21:28 | 2 | 4 | 0 | 単発×6 |
| 合計 | 225 | 185 | 47 | |
検証結果
| ガチャ回数等 | |
|---|---|
| ガチャ回数 | 457回 |
| 単発ガチャ回数 | 6回 |
| 「10回+1ガチャ」の回数 | 41回 |
| 消費ジュエル数 | 1万400個 |
| iOSでの最安値 | 15万6000円 |
| Androidでの最安値 | 16万8480円 |
| ★2 | ★3 | ★4 | |
|---|---|---|---|
| 出現回数 [回] | 225 | 185 | 47 |
| 出現比率 [%] | 49.2 | 40.5 | 10.3 |
| d [%] | 4.6 | 4.5 | 2.8 |
| 信頼度95%の 信頼区間 [%] | 44.6~53.9 | 35.9~45 | 7.4~13.1 |
信頼区間をある範囲に収めるのに必要なガチャ回数
信頼度95%の信頼区間を(R-d)~(R+d)の間に収めたいときのガチャ回数nは、★4排出率のおよその値をRとして
d>1.96√(R(1-R)/n)
をnについて解くことで得られます。すなわち
n>3.84R(1-R)/d^2
です。
例えば、おそらく★4排出率が5%だと予想して、信頼度95%の信頼区間を(5-0.7)%~(5+0.7)%の範囲に収めたいとき、必要なガチャ回数は
n>3.8400×5%×(1-5%)÷0.7%^2=3722.4…
より、約3730回以上です。
逆に見れば、3730回回したときの★4の出現比率が5%だった時、★4排出率の信頼度95%の信頼区間がおよそ4.3%~5.7%であることを意味します。
この必要なガチャ回数をdと排出率の推定値を変えて表したのが下のグラフです。
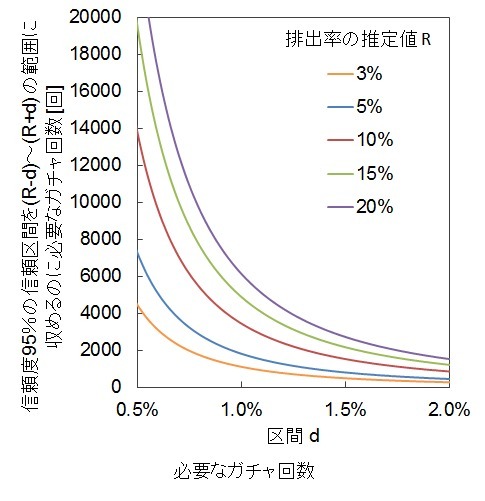
表
| d [%] | 信頼度95%の信頼区間を (R-d)~(R+d)の範囲に収めるのに必要なガチャ回数 | |||||||
|---|---|---|---|---|---|---|---|---|
| ★4排出率のおよその値 R [%] | ||||||||
| 3 | 4 | 5 | 6 | 8 | 10 | 12 | 15 | |
| 0.3 | 12500 | 16400 | 20300 | 24100 | 31500 | 38400 | 45100 | 54400 |
| 0.5 | 4470 | 5900 | 7300 | 8670 | 11400 | 13900 | 16300 | 19600 |
| 0.7 | 2290 | 3010 | 3730 | 4420 | 5770 | 7060 | 8280 | 10000 |
| 0.8 | 1750 | 2310 | 2850 | 3390 | 4420 | 5400 | 6340 | 7650 |
| 0.9 | 1380 | 1830 | 2260 | 2680 | 3490 | 4270 | 5010 | 6050 |
| 1.0 | 1120 | 1480 | 1830 | 2170 | 2830 | 3460 | 4060 | 4900 |
| 1.1 | 924 | 1220 | 1510 | 1790 | 2340 | 2860 | 3360 | 4050 |
| 1.2 | 776 | 1030 | 1270 | 1510 | 1970 | 2400 | 2820 | 3400 |
| 1.3 | 662 | 873 | 1080 | 1290 | 1680 | 2050 | 2400 | 2900 |
| 1.5 | 497 | 656 | 811 | 963 | 1260 | 1540 | 1810 | 2180 |
| 2.0 | 280 | 369 | 456 | 542 | 707 | 864 | 1020 | 1230 |
| 2.5 | 179 | 236 | 292 | 347 | 453 | 553 | 650 | 790 |
| 3.0 | - | 164 | 203 | 241 | 315 | 384 | 460 | 550 |
| 3.5 | - | - | 149 | 177 | 231 | 283 | 340 | 400 |
| 4.0 | - | - | 114 | 136 | 177 | 216 | 260 | 310 |
| 4.5 | - | - | - | 107 | 140 | 171 | 210 | 250 |
| 5.0 | - | - | - | - | 114 | 139 | 170 | 200 |
1より十分に小さいRの場合
定数kを用いて
d=kR (0<k<1)
と表すことにします。
このとき、信頼度95%の信頼区間を(1-k)R~(1+k)Rの間に収めたいときのガチャ回数nは
n>3.84(1-R)/(k^2*R)
となります。
ここでRが1より十分に小さいとき、R/(1-R)≒Rの近似を使うことができるので、この式は
n>3.84/(k^2*R)
と表すことができます。
これは、信頼度95%の信頼区間を(1-k)R~(1+k)Rとしたいとき、★4排出率のおよその値の逆数の(3.84/k^2)倍が必要なガチャ回数であるということを意味します。
例:★4排出率のおよその値が1%、k=0.2とした場合
信頼度95%の信頼区間を0.8%~1.2%の間に収めるのに必要なガチャ回数は
3.84/(0.2^2*1%)=9600
より9600回
式に出てくるn回だけガチャを回したときに★4が出現する回数は
nR=3.84/(k^2*R)*R=3.84/k^2
となります。
言い換えると、(3.84/k^2)回★4が出現すればその信頼度95%の信頼区間が(1-k)R~(1+k)Rとなります。
★4が出現する回数をaとすれば
k=√(3.84/a)=1.96/(√a)
と計算できます。
例:★4排出率のおよその値Rが1より十分に小さく、k=0.2とした場合
信頼度95%の信頼区間を0.8R~1.2Rの間に収めるのに必要な★4の出現回数は
3.84/0.2^2=96
より96回
例:★4排出率のおよその値Rが1より十分に小さく、★4が10回出現した場合
信頼度95%の信頼区間を(1-k)R~(1+k)Rと表記するときのkは
1.96/(√10)=0.6198…
より約0.62
kを横軸にとりaを求めたものが下のグラフです。
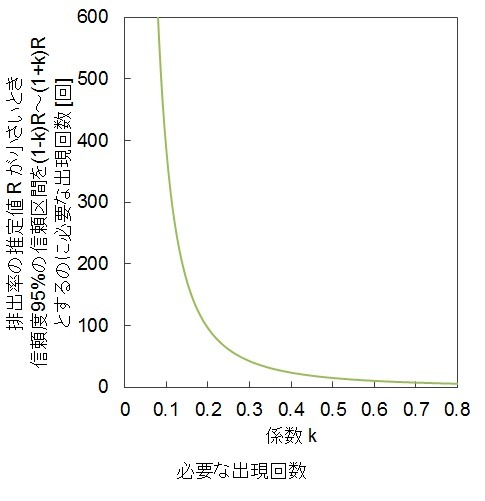
| k | a=3.84/k^2 |
|---|---|
| 0.05 | 1536 |
| 0.075 | 683 |
| 0.1 | 384 |
| 0.125 | 246 |
| 0.15 | 171 |
| 0.2 | 96 |
| 0.3 | 43 |
| 0.5 | 15 |
| 0.6 | 11 |
| 0.7 | 8 |
| 0.8 | 6 |
| a | k=1.96/√a |
|---|---|
| 6 | 0.80 |
| 7 | 0.74 |
| 8 | 0.69 |
| 9 | 0.65 |
| 10 | 0.62 |
| 12 | 0.57 |
| 15 | 0.51 |
| 20 | 0.44 |
| 50 | 0.28 |
| 100 | 0.20 |
| 200 | 0.14 |
| 500 | 0.088 |
| 1000 | 0.062 |
1より十分に小さいとはいえないRの場合
Rが1より十分に小さいとは言えない場合、信頼度95%の信頼区間を(1-k)R~(1+k)Rの間に収めたいときの★4の出現回数aは
a>3.84(1-R)/(k^2)
です。(1-R)<1から、Rが1より十分に小さいときよりもaは少なくなります。
結論
排出率のおよその値をRとして信頼度95%の信頼区間を0.8R~1.2Rの間に収めるのは現実的に有用であると思われます。
したがって、一般的なガチャにおいて
排出率を推定したいレアリティのアイテムを100回以上出現させると
有用な排出率の推定値が得られる
ということを覚えておくとよさそうです。
-
-

-
冒険者さん
-
-
-

-
冒険者さん
-
-
-

-
冒険者さん
1010年まえ ID:tmuhhe5vいやいや理屈を述べないで大体こんくらいっすねなんて信用出来んだろ。これはホントに助かる
-
-
-

-
冒険者さん
910年まえ ID:r9zacu83年代的に子供も多いしイミフなのもしょうがないやろ
大学くらいになれば統計学の偉大さが分かるはず
-
-
-

-
冒険者さん
810年まえ ID:kdqujbke187+単発20回くらいでシャルなし
・・・ということは俺も641回回せってことなのかね・・・。
-
-
-

-
冒険者さん
710年まえ ID:hmj11601オウガ狙いで66連してシャルは3、オウガ無し・・・。
武器みたいに星4×4人と交換してくれんかね。
-
-
-

-
冒険者さん
610年まえ ID:rijit2vo久々にお詫びのジュエルで11連1回やったらシャル2だったから出やすいのかと思ってた
-
-
-

-
冒険者さん
510年まえ ID:mt8c3qtzだらだらと書きすぎて読む気がしない
☆2約50% ☆3約40% ☆4約10%
この1行だけでいいよ
-
-
-

-
冒険者さん
410年まえ ID:kh23tjs3心を慰めるために失敗の理屈を知りたい人もいるんだよ
意味の分からん人はただ悔しがるのみ
-
-
-

-
冒険者さん
310年まえ ID:jjqgxmqd分かりやすいからいいと思うよ。
知らん人には信頼区間?クソワロとか思う人いるだろうけどね。
-
















































