☆4が出る確率の考察
目次 (ガチャの確率)
- ガチャの確率について
- キャラガチャについて
- 武器ガチャについて
- 要点
- ★4排出率=10% と仮定した場合
- ガチャとレアリティ
- 共通
- 職業について
- 種類の数
- キャラガチャ
- 限定キャラ
- キャラガチャの出現確率の変更
- 武器ガチャ
- 限定・記念武器
- 武器ガチャの出現確率及び仕様の変更
- ジュエル数・価格への換算
- 注意事項
- ガチャの性質
- ガチャのシミュレーション
- ★4排出率の推定
- ★4排出率を仮定した場合の確率と期待値
- ガチャの確率分布
- 1回以上出現する確率
- ある回数以上出現する確率
- 1点狙いが成功する確率
- 1点狙いが成功する確率がある確率となるまでにガチャを回す回数
- ある確率でやめる場合の期待値
- あるガチャ回数でやめる場合の期待値
- 現実的な期待値に対する倍率
- 2点狙いが成功する確率
- 1点狙いが成功する確率が分かっているときの2点狙い・3点狙いが成功する確率
- 狙いが成功する確率がある確率となるまでにガチャを回す回数
- 各狙いの現実的な期待値に対する倍率
- 狙いが成功する確率からガチャ回数を暗算で導く方法
- その他の確率
- ガチャ確率の計算式一覧
ガチャの確率について
2017年7月14日にキャラガチャ・武器ガチャの提供割合設定が開示された。
キャラガチャについて
「ゼロ・クロニクルガチャ」「凱旋キャラガチャ8種類」全てにおいて、以下の提供割合設定が行われている。
◇同率レアリティの各キャラの提供割合は、均等に設定しています。
| レアリティごとのキャラ提供割合 | |||
|---|---|---|---|
| ★5ありガチャ | ★5なしガチャ | ||
| ★5 | 1% | ★5 | 無し |
| ★4 | 10% | ★4 | 10% |
| ★3 | 40% | ★3 | 40% |
| ★2 | 49% | ★2 | 50% |
武器ガチャについて
「ゼロ・クロニクルガチャ」「凱旋キャラガチャ8種類」全てにおいて、以下の提供割合設定が行われている。
◇同率レアリティの各武器の提供割合は、均等に設定しています。
| レアリティごとの武器提供割合 | |||
|---|---|---|---|
| ★5ありガチャ | ★5なしガチャ | ||
| ★5 | 4% | ★5 | 無し |
| ★4 | 8% | ★4 | 8% |
| ★3 | 42.2% | ★3 | 42.2% |
| ★2 | 45.8% | ★2 | 49.8% |
要点
武器ガチャには特定の★4武器がいきなり★5でも登場するキャンペーンが行われることがある
武器ガチャ10連で最後の一つが★4確定するキャンペーンが行われることがある
どちらの場合でも進化の1段階目のレアリティが★4の武器の出現回数の期待値が上がることになる
武器ガチャ10連の最安値は
2250円
キャラガチャ「10回+1ガチャ」の最安値は
3750円
運営が★4排出率(=ガチャが★4のキャラか武器を排出する確率)またはガチャシステムを変えない限り、
ガチャを1回回したときに★4が出現する確率は常に一定
★4排出率は95%の確率で
8.4%~11.1%
の間にある
★4が出現する回数の期待値は
(ガチャ回数)×(★4排出率)
★4排出率がp%のガチャをn回回したとき、★4がa回出現する確率[%]はExcel上で
=BINOM.DIST(a,n,p%,FALSE)*100
★4が1回出現するまでにガチャを回す回数の期待値は
1÷(★4排出率)
★4の1点狙いが成功するまでにガチャを回す回数の期待値は
(★4の種類の数)÷(★4排出率)
★4の1点狙いが成功する確率が95%となるまでにガチャを回す回数のおよその数は
(★4の種類の数)÷(★4排出率)×3
★4排出率=10% と仮定した場合
ガチャを11回回したとき、★4が1回以上出現する確率は
約69%
ガチャに★4が16種類あるとき、★4の1点狙いが成功するまでにガチャを回す回数の期待値は
160回
ガチャに★4が16種類あるとき、★4の1点狙いが成功するまでにガチャを回す回数の期待値の値段は
約5万5000円
ガチャに★4が16種類あるとき、★4の1点狙いが成功する確率が95%となるまでにガチャを回す回数は
約480回
ガチャに★4が8種類あるとき、★4の1点狙いが成功するまでにガチャを回す回数の期待値、
または、ガチャに★4が16種類あるとき、特定の2種類の★4のどちらかを引き当てるまでにガチャを回す回数の期待値は
80回
ガチャに★4が8種類あるとき、★4の1点狙いが成功する確率が95%となるまでにガチャを回す回数、
または、ガチャに★4が16種類あるとき、特定の2種類の★4のどちらかを引き当てる確率が95%となるまでにガチャを回す回数は
約240回
ガチャに★4が16種類あるとき、特定の2種類の★4を両方とも引き当てるまでにガチャを回す回数の期待値は
240回
ガチャに★4が8種類あるとき、★4をすべて引き当てるまでにガチャを回す回数の期待値は
約220回
ガチャとレアリティ
白猫プロジェクトのガチャには、キャラガチャと武器ガチャの2種類があります。
共通
- ガチャから出現するときのレアリティは、★2、★3、★4の3段階です。
- ★5(★4キャラ・武器が育成された状態)で出現するガチャも存在します。
- 通常のキャラ・武器と、限定のキャラ・武器があります。
- 運営はガチャの出現確率を公表していませんでした。
- 単発と連続で引いた場合で出現確率は変わりません。
- 特定の期間にガチャイベントが被る場合、排出内容が独立した2つ以上のガチャが同時に開催されることがあります。
職業について
- ガチャには通常時では8種類の職業のキャラまたは武器が登場します。
- 双剣はフォースター☆プロジェクト9thのガチャから実装されました。
- ドラゴンライダーは白猫プロジェクト一周年記念キャラから実装されました。
- ドラゴンライダー武器は初めは配布のみでガチャには登場しませんでした。
- ドラゴンライダー武器はBrave The Lion 2の限定武器で初めてガチャに登場しました。
- フォースター☆プロジェクトリベンジwithアニゲラ!のガチャから通常でもドラゴンライダーが登場するようになりました。
- これ以前のドラゴンライダーは限定のみです。
- ヴァリアントは2016年4月26日16:00から実装されました。
- ヴァリアントは現在フォースター☆プロジェクトには登場しません。
- バーサーカーは2017年7月14日16:00から実装されました。
- バーサーカーは現在フォースター☆プロジェクトには登場しません。
種類の数
- 各ガチャには下の表に示した数だけ種類があります。
- ガチャから★2の双剣とドラゴンライダー(武器)は出現しません。★3、★4の双剣とドラゴンライダー(武器)は出現します。
- 通常はガチャから★2、★3、★4のヴァリアント(武器)は登場しません。
- ヴァリアント(武器)が登場するのは運営がそのことを告知したときです。
- (日時不明)ヴァリアント★2、★3、★4アイオロスシリーズヴァリアント(武器)が常時排出されるようになりました。
- 括弧内は★3の双剣とドラゴンライダー(武器)とヴァリアント(武器)を除く1職あたりの種類の数です。
- ★3の双剣とドラゴンライダー(武器)はそれぞれ2種類です。
- 下の表に示した以外の組み合わせでガチャが実装されることもあります。
| ※旧情報 | ★2 | ★3 | ★4 | 合計 |
|---|---|---|---|---|
| キャラガチャ (通常時、入れ替え限定キャラ登場時) | 18 (3) | 28 (4) | 16 (2) | 62 |
| キャラガチャ (ヴァリアント登場時) | 18 (3) | 28 (4) | 18 (2) | 64 |
| 限定キャラガチャ | 18 (3) | 28 (4) | 8 (1) | 54 |
| 武器ガチャ (通常時) | 18 (3) | 22 (3) | 24 (3) | 64 |
| 武器ガチャ (入れ替え限定キャラのモチーフ武器登場時) | 18 (3) | 22 (3) | 25~28 (3 or 4) | 65~68 |
| 武器ガチャ (限定キャラガチャのモチーフ武器登場時) | 18 (3) | 22 (3) | 32 (4) | 72 |
| 武器ガチャ (ヴァリアント登場時) | 20 (3) | 25 (3) | 26 (4) | 71 |
キャラガチャ
- 単発のほかに、11連(10回+1ガチャ)でも回すことができます。
- 単発の場合、1回あたり25ジュエルを使用します。
- 10回+1ガチャの場合、250ジュエルを使用します。
- キャラクターは友情覚醒をすると、★2、★3、★4はそれぞれ★3、★4、★5にレアリティが1つ上がります。
- 出現するときに金色か銀色のマントを羽織ったキャラが空から降ってきます。
- 最後の色が銀色だった場合、そのキャラのレアリティは★2です。
- 最後の色が金色だった場合、そのキャラのレアリティは★3か★4です。
- 名星会キャラクターが★5で排出される場合、赤色のマントを羽織った状態になります。
- すでに所持しているキャラクターをガチャで引くと、キャラクターが虹のルーンを持って現れます。この虹のルーンをキャラクターに使うことで、キャラクターを限界突破することができます。
- キャラクターの所持数制限はありません。
- キャラクターの交換システムはありません。
- フォースタープロジェクトで1位と2位になったキャラは次のフォースタープロジェクトまでの間ガチャに登場します。
- フォースタープロジェクトで3位になったキャラはガチャから登場しなくなります。
限定キャラ
- 2017/01/17以降に登場した同形式のガチャについては、オーバードライブ紅蓮ガチャ以外、再登場する場合があると明記されている。そのためゲーム内でも限定キャラと呼称されないが、説明が煩雑になるためこの項では限定キャラと呼ぶ。
- 新しいキャラクターが、同数のフォースターキャラと入れ替えられる形式の、限定のキャラガチャが登場することがあります。
- 限定キャラが登場している期間は、限定キャラと同じ職業の、直前のフォースター☆プロジェクトで2位だったキャラクターが登場しません。
- 2017年1月17日(名星会版カモメ)以降、限定★4キャラクターが★5(友情覚醒済のレベル100)で登場することがあるガチャも存在します。
- 新フォースター☆プロジェクト以降は、職業関係なく直前のフォースター☆プロジェクトで下位のキャラが登場しません。
- 1または2, 4体が限定キャラとして登場します。
- ★4キャラクターが新キャラのみでフォースターキャラが排出されない、限定のキャラガチャが設置されることがあります(別枠)。
- ★2、★3は通常のキャラガチャと同じです。
- ★4の職業ごとの人数は各ガチャごとに固有です。職業が重複するケースも存在します。
- ★4の出現確率は通常と同じです。
キャラガチャの出現確率の変更
- 2015年2月28日 20:00より、★4キャラクターの出現確率が2倍に変更されました。これに従い、★2キャラクターの出現確率が低下しました。
武器ガチャ
- 単発のほかに5連と10連でも回すことができます。
- 1回あたり15ジュエルを使用します。
- 武器は進化の3段階目なるように進化合成すると、レアリティが1つ上がります。
- ★3武器は進化の4段階目になるように進化合成すると、レアリティが★5になります。
- 出現するときに金色か銀色にモニュメントが光ります。
- 最後の色が銀色だった場合、その武器のレアリティは★2です。
- 最後の色が金色だった場合、その武器のレアリティは★3か★4です。
- ★4は、1職あたり2種類がモチーフ武器です。
- 残りの1種類は定期的に入れ替えられるシリーズものの非モチーフ武器です。
- 非モチーフ武器の入れ替え周期は数か月です。
- 武器はすでに所持している武器と同じものが出現しても、そのまま2つ目の武器として受け取れます。
- 武器はガチャを回して所持数の上限を超えた分がプレゼントボックスへ送られます。
- 出現時のレアリティが★4の武器を4つ集めると、武器交換所で好きな★4の武器1つと交換することができます。
- ガチャ画面で表示される武器のステータスは、進化の初期段階のLv1のものです。
- フォースタープロジェクトで勝ち残ったキャラのモチーフ武器は次のフォースタープロジェクトまでの間ガチャに登場します。
- フォースタープロジェクトで敗退したキャラのモチーフ武器は、武器ガチャ更新のタイミングでガチャに登場しなくなります。
限定・記念武器
- 限定キャラの武器が追加されたガチャが登場することがあります。
- 限定の武器が登場している期間でも、通常の武器は引き続き登場します。
- フォースターキャラの武器が登場せす、★4武器は新武器のみ排出される別枠形式の限定武器ガチャが設置されたことはありません。
- 限定キャラガチャが同時に2種以上ある場合、限定キャラの武器が追加された2種類以上のガチャが同時に登場することがあります。
- 2017年7月14日開催の★4キャラ・武器プレゼントでの扱いより、ゴエティアシリーズは限定・記念武器として扱われています。
武器ガチャの出現確率及び仕様の変更
- 2015年7月2日 16:00より、★4武器の出現確率が2倍に変更されました。これに従い、★2武器の出現確率が低下しました。
- 期間中、一部の★4武器が★5としていきなり登場するキャンペーンが実施されることがあります。
- ★5武器登場中は★2武器の出現確率が低下します。
- ★3武器、★4武器の出現確率に変更はありません。
- ★4武器も引き続き登場します。
- ★5武器は武器交換で入手することはできません。
- チュートリアル中の武器ガチャからは★5武器は登場しません。
- 期間中、武器ガチャ10連で最後の一つが★4確定するキャンペーンが実施されることがあります。
ジュエル数・価格への換算
消費ジュエル数及びジュエル価格は変更される可能性があります。必ずゲーム内のお知らせ、価格表示等をご確認ください。
白猫プロジェクトでは、<ガチャ・ショップ>画面からジュエルを購入することができます。
| ジュエル数 | 価格 [円] | ||||
|---|---|---|---|---|---|
| iOS | Android | ||||
| ジュエル 1つあたり | ジュエル 1つあたり | ||||
| 最高値 | 5 | 120 | 24 | 108 | 21.6 |
| 最安値 | 360 | 5400 | 15 | 5832 | 16.2 |
ガチャ回数に以下の値をかけることで、必要なジュエル数または価格を計算することができます。
| ガチャの種類 | ガチャ1回 の消費 ジュエル数 | ガチャ1回の価格 [円] | |||
|---|---|---|---|---|---|
| iOS | Android | ||||
| 最安値 | 最高値 | 最安値 | 最高値 | ||
| キャラ(単発) | 25 | 375 | 600 | 405 | 540 |
| キャラ(10回+1) | 22.7 | 340.9 | 545.5 | 368.2 | 490.9 |
| 武器 | 15 | 225 | 360 | 243 | 324 |
※値は小数第2位を四捨五入したものです。
クエストクリア報酬でもらえるジュエル数はこちら
注意事項
- このページでは、「★4」という場合、ガチャで出現するときのレアリティが★4の武器またはキャラクターを指すことにします。
- 便宜上★4と呼びますが、ガチャの排出率はわからないのですから、実測したキャラガチャの結果と武器ガチャの結果を混合するべきではありません。
- キャラクターの場合、特に指定の無い限り、★4が虹のルーンに変わる・変わらないにかかわらず「★4が1回出現する」と数えます。
- 確率はガチャを単発で回した場合です。
- 運営が定めた★4の出現確率と、計算によって求められる出現確率の混同を避けるため、運営が定めた「★4をガチャが排出する確率」を「★4排出率」と呼び、以降これを用いることにします。
- (★4以外を排出する確率)=1-(★4排出率)です。
- A^Bという表記は「AのB乗」という意味です。
- ★4排出率は、運営が告知した場合を除いて、常に一定とします。
- 同じガチャを回したとき、★4の1種類が出現する確率は、どの★4でも同じだとします。
- 以下の計算式および表の値は数学的なものであり、キャラガチャ・武器ガチャにかかわらず成り立ちます。
- ★4を★2、★3★5に読み替えても成り立ちます。
- ただし、武器ガチャが「いきなり★5」イベント期間のとき、★4を「★4または★5」に読み替えた場合、「★4または★5」の種類の数を用いる確率の計算式・表の値は成り立ちません。
- また、★4を該当のレアリティのアイテムに読み替えれば、白猫プロジェクト以外の一般的なガチャにも適用できます。
- ★4排出率を推定するとき、リセマラをした場合、リセマラとして回した中で必ず1回は★4が出現しているわけですから、リセマラ分のデータは除外すべきです。
- ★4排出率を除く主な確率の有効数字は小数第1位までです。
- 100.0%という表記は「確率99.95%以上」、0.0%という表記は「確率0.05%未満」という意味です。
- ただし、小数点のつかない100%・0%は、必ず起こること・決して起こらないことを表すことにします。
ガチャの性質
くじ引きとの違い
現実のカプセルトイ(ガチャガチャ)やくじ引きには、くじと景品に有限な個数が用意されています。
カプセルトイにどうしてもほしいものがあっても、無くなってしまえば引けません。
福引きではすべてのくじ(玉)が出尽くせば、誰かしらに1等賞が当たります。
おみくじで中身を変えなければ、いつか誰かが大吉を引くでしょう。
毎年どこかの宝くじで、億単位のお金を当てる人がいます。
どのくじも引き尽くせば、誰かが必ず当たりを引けるシステムです。逆に言えば、他の誰かが必ずはずれを引くシステムです。
しかし、ソーシャルゲームで展開される仮想的なガチャというシステムには、その景品の個数に制限がありません。ガチャ回数にも制限がありません。
当然ガチャを回し尽くすことはできません。
ですから、当たりが確定する枠を作らない限り、全員が外れを引く可能性があります。逆に、全員が当たりを引く可能性があります。(どちらの可能性も限りなく0に近いです)
これは、ガチャが前回の結果に依らず、常に一定の確率で景品(アイテム)を排出しているからです。
例えば、カプセルトイを直前に回した人がレアアイテムを手に入れたとき、次に自分が回してそのレアアイテムを入手できる可能性は、直前に回した人よりも低くなります。
ソーシャルゲームのガチャを直前に回した人がレアアイテムを手に入れたとき、次に自分が回してそのレアアイテムを入手できる可能性は、直前に回した人と同じです。
ガチャにおける確率は、カプセルトイやくじ引きの確率よりも、コインやさいころを投げたときの確率に似ています。
一様な確率
★4排出率は運営が変更をしない限り、常に一定です。次のガチャを回して★4が出現する確率は、その前に回したガチャの結果にかかわらず、常に★4排出率と一致します。
例えば、★4排出率が10%のガチャを10回回したときを考えます。
1回目に★4が出現する確率は10%です。2回目に★4が出現する確率は、1回目に★4が出る・出ないによらず、10%です。10回目に★4が出現する確率は、もちろん10%です。
別の見方をして、10回以内に★4が1回でも出現する確率を求めると、65.1%となります。
仮に、9回連続で★4が出なかった場合、「もうそろそろ出てほしい」と思うかもしれませんが、10回目に★4が出現する確率が65.1%になるわけではありません。
当然、10回目に★4が出る確率は10%であることに変わりません。
10回目を0回目と数え直せば、今後10回以内に★4が1回でも出現する確率は、やはり65.1%です。
ランダムの認識
人はランダムに起こるはずの現象にパターンを感じることがあります。
下の図は32×32個の四角形を、■:□=1:9となるようにランダムに敷き詰めたものです。
単発と連続
白猫プロジェクトではキャラと武器のどちらも単発と連続のガチャを回すことができます。それでは、単発と連続どちらのガチャを回した方がよいのでしょうか。
武器ガチャの場合、単発、5連、10連の中から選ぶことができ、1回武器が出現する当たりの消費ジュエル数は同じです。どれでもいくつでもいいから★4が出てほしいと思うなら、どれを選んでも同じです。特定の武器を狙っている場合では、単発で回したときはその武器が出た時点でガチャを回すのをやめてよいのですから、連続で回したときはその武器が出た後に出現した分は不要だったことになります。したがって、ほしい武器があってほかの武器がいらない場合は単発で回した方がよいことになります。
キャラガチャの場合、単発、10回+1ガチャのどちらかを選ぶことができ、1回キャラが出現する当たりの消費ジュエル数は10回+1ガチャのほうが少ないです。どの★4が出てもいいと思うなら、ジュエル効率のよい10回+1ガチャを選ぶべきです。特定の★4キャラを狙っている場合、そのキャラが出現するまでにまでにガチャを回す回数の期待値が問題になります。★4排出率が10%のガチャに★4が7種類あるとき、1種類を狙うような場合ではその期待値は70回となります。これは10回+1ガチャの出現回数11回よりも多くなりますから、ほしいキャラがある場合も10回+1ガチャを回した方がよいことになります。
ガチャのシミュレーション
白猫キャラガチャシミュレーター
武器ガチャシミュレーター
白猫x黒猫コラボガチャシミュレーター
茶熊学園2015キャラガチャシミュレーター
2016年お正月キャラガチャシミュレーター
2015年クリスマスキャラガチャシミュレーター
★4確定 白猫キャラガチャシミュレーター
白猫温泉物語キャラガチャシミュレーター
白猫ダグラス2キャラガチャシミュレーター
七つの大罪コラボキャラガチャシミュレーター
★4排出率をp%と仮定するとき、次のようにExcel上に入力して連続コピーをすることにより、簡易的なガチャのシミュレーションをすることができます。
=IF(RAND()<p%,"★","☆")
★4を「★」、★4以外を「☆」に見立てています。
※操作をするごとに結果が変わります。
計算もしたいときには、次のように入力して連続コピーします。
=IF(RAND()<p%,1,0)
連続コピーした範囲を、
- COUNT関数を使って求めた個数がガチャ回数です。
- SUM関数を使って求めた合計が出現回数です。
- AVERAGE関数を使って求めた平均が比率です。
※関数を使わなくても、範囲を選択すれば、下のステータスバーに平均、データの個数、合計が表示されます。
★4排出率の推定
排出率の推定のページへ
★4排出率を仮定した場合の確率と期待値
下記の情報は、★4排出率を仮定した場合です。
ガチャの確率分布
出現回数の期待値と分散
ガチャを回した結果を、「★4が出現する」と「★4以外が出現する」に分けるとします。一般的なガチャを回すことは独立な試行です(ガチャを回したある結果がガチャを回したほかの結果に影響しない)。★4排出率が一定だとすると、その確率分布は二項分布になります。
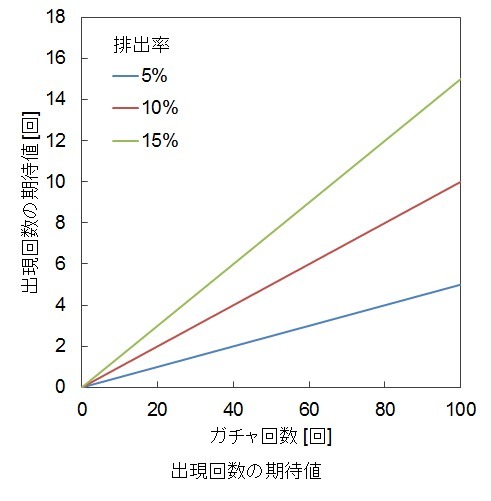
ある回数ガチャを回したとき、★4が出現する回数の期待値は、
(ガチャ回数)×(★4排出率)
で表されます。
例:★4排出率が10%のガチャを22回回した場合
★4が出現する回数の期待値は
20×10%=2.2
より2.2回
期待値は下図のようにガチャ回数に比例します。
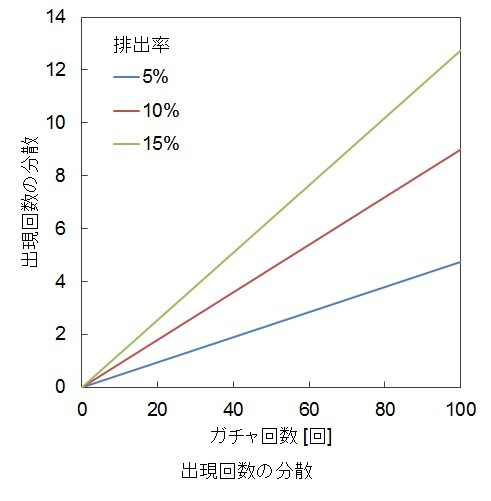
データのばらつき具合を表す分散は
(ガチャ回数)×(★4排出率)×(★4以外を排出する確率)
となります。
式からわかるように、ガチャ回数が増加すると、★4の出現回数の分散も増加します。言い換えれば、ガチャを回せば回すほど、★4の出現回数のばらつき具合が大きくなります。
さらに、一般に★4排出率は0.5以下だと考えられますから、★4排出率が大きくなるときも★4の出現回数のばらつき具合は大きくなります。
この分散は下のグラフのようにガチャ回数に比例します。
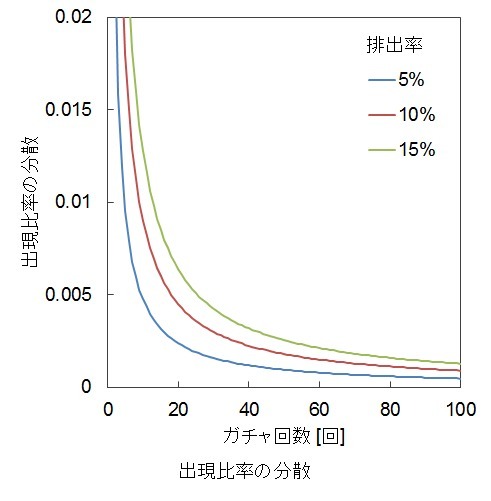
変数を★4の出現回数から、★4の出現回数の比率に変えてみます。すると変数は
(★4の出現回数の比率)=(★4の出現回数)/(ガチャ回数)
となり、その期待値は
(★4排出率)
そのものです。
★4の出現回数の比率の分散は、確率変数の関係式から
(★4排出率)×(★4以外を排出する確率)/(ガチャ回数)
となります。これは、ガチャ回数が増加すると、★4の出現回数の比率の分散が0に近づいていくことを示しています。言い換えると、ガチャを回せば回すほど、★4の出現回数の比率は★4排出率に近づいていきます。
一般には、試行回数を重ねると事象が実現する回数が理論上の値に近づくことを大数の法則と呼びます。
出現比率の分散は下のグラフのようにガチャ回数に反比例します。
ガチャ確率の計算式
★4排出率がp%のガチャをn回回したときに、★4がa回出現する確率[%]はExcel上で次の式で表せます。
=BINOM.DIST(a,n,p%,FALSE)*100
例:★4排出率が10%のガチャを22回回したとき★4が2回出現する確率を求めたい場合
Excelに次のように入力
=BINOM.DIST(2,22,10%,FALSE)*100
すると値が28.08…と出てくるので、求める確率は約28.1%と分かる
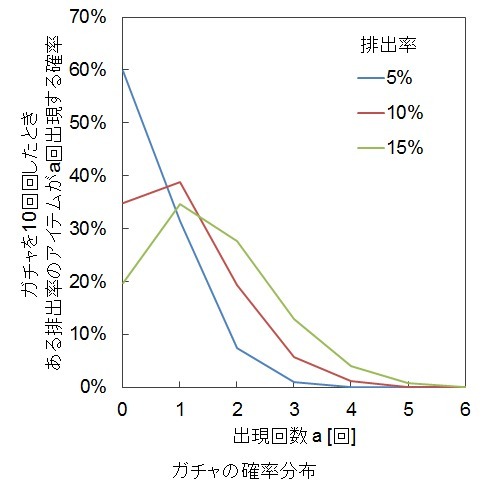
ガチャを10回回したときと100回回したときの分布を下の図に示します。
10回回したとき
100回回したとき
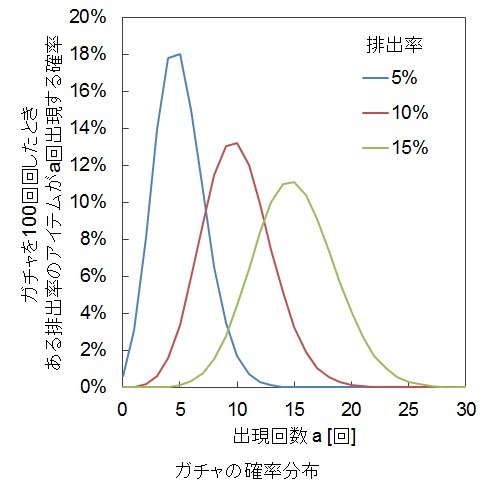
なお、FALSEをTRUEに変えてExcelに次のように入力すると、★4排出率がp[%]のガチャをn回回したときに、★4が出現するのがa回以下である確率[%]を求められます。
=BINOM.DIST(a,n,p%,TRUE)*100
| ★4の 出現回数 =a | 10回ガチャを回したとき ★4がa回出現する確率 [%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0 | 59.9 | 34.9 | 19.7 |
| 1 | 31.5 | 38.7 | 34.7 |
| 2 | 7.5 | 19.4 | 27.6 |
| 3 | 1.0 | 5.7 | 13.0 |
| 4 | 0.1 | 1.1 | 4.0 |
| 5以上 | 0.0 | 0.2 | 1.0 |
| 出現回数 の期待値 | 0.5 | 1.0 | 1.5 |
| ★4の 出現回数 =a | 11回ガチャを回したとき ★4がa回出現する確率 [%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0 | 56.9 | 31.4 | 16.7 |
| 1 | 32.9 | 38.4 | 32.5 |
| 2 | 8.7 | 21.3 | 28.7 |
| 3 | 1.4 | 7.1 | 15.2 |
| 4 | 0.1 | 1.6 | 5.4 |
| 5以上 | 0.0 | 0.3 | 1.6 |
| 出現回数 の期待値 | 0.6 | 1.1 | 1.7 |
| ★4の 出現回数 =a | 22回ガチャを回したとき ★4がa回出現する確率 [%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0 | 32.4 | 9.8 | 2.8 |
| 1 | 37.5 | 24.1 | 10.9 |
| 2 | 20.7 | 28.1 | 20.1 |
| 3 | 7.3 | 20.8 | 23.7 |
| 4 | 1.8 | 11.0 | 19.9 |
| 5 | 0.3 | 4.4 | 12.6 |
| 6 | 0.1 | 1.4 | 6.3 |
| 7以上 | 0.0 | 0.4 | 3.7 |
| 出現回数 の期待値 | 1.1 | 2.2 | 3.3 |
| ★4の 出現回数 =a | 55回ガチャを回したとき ★4がa回出現する確率 [%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0 | 6.0 | 0.3 | 0.0 |
| 1 | 17.2 | 1.9 | 0.1 |
| 2 | 24.5 | 5.6 | 0.6 |
| 3 | 22.8 | 11.0 | 1.9 |
| 4 | 15.6 | 15.8 | 4.3 |
| 5 | 8.4 | 17.9 | 7.8 |
| 6 | 3.7 | 16.6 | 11.5 |
| 7 | 1.4 | 12.9 | 14.2 |
| 8 | 0.4 | 8.6 | 15.0 |
| 9 | 0.1 | 5.0 | 13.8 |
| 10 | 0.0 | 2.6 | 11.2 |
| 11 | 0.0 | 1.2 | 8.1 |
| 12 | 0.0 | 0.5 | 5.3 |
| 13 | 0.0 | 0.2 | 3.1 |
| 14 | 0.0 | 0.1 | 1.6 |
| 15以上 | 0.0 | 0.0 | 1.3 |
| 出現回数 の期待値 | 2.8 | 5.5 | 8.3 |
| ★4の 出現回数 =a | 110回ガチャを回したとき ★4がa回出現する確率 [%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0 | 0.4 | 0.0 | 0.0 |
| 1 | 2.1 | 0.0 | 0.0 |
| 2 | 5.9 | 0.1 | 0.0 |
| 3 | 11.2 | 0.3 | 0.0 |
| 4 | 15.7 | 0.8 | 0.0 |
| 5 | 17.5 | 1.9 | 0.0 |
| 6 | 16.1 | 3.7 | 0.1 |
| 7 | 12.6 | 6.2 | 0.3 |
| 8 | 8.6 | 8.8 | 0.7 |
| 9 | 5.1 | 11.1 | 1.3 |
| 10 | 2.7 | 12.5 | 2.4 |
| 11 | 1.3 | 12.6 | 3.8 |
| 12 | 0.6 | 11.5 | 5.5 |
| 13 | 0.2 | 9.7 | 7.4 |
| 14 | 0.1 | 7.4 | 9.0 |
| 15 | 0.0 | 5.3 | 10.2 |
| 16 | 0.0 | 3.5 | 10.6 |
| 17 | 0.0 | 2.1 | 10.4 |
| 18 | 0.0 | 1.2 | 9.5 |
| 19 | 0.0 | 0.7 | 8.1 |
| 20 | 0.0 | 0.3 | 6.5 |
| 21 | 0.0 | 0.2 | 4.9 |
| 22 | 0.0 | 0.1 | 3.5 |
| 23 | 0.0 | 0.0 | 2.4 |
| 24 | 0.0 | 0.0 | 1.5 |
| 25以上 | 0.0 | 0.0 | 2.0 |
| 出現回数 の期待値 | 5.5 | 11.0 | 16.5 |
1回以上出現する確率
ガチャをある回数回すまでに★4が1回以上出現する確率は
1-(★4以外を排出する確率)^(ガチャ回数)
です。
★4が1回出現するまでにガチャを回す回数の期待値は
1/(★4排出率)
です。
例:★4排出率が10%のガチャを回す場合
22回目までに★4が1回以上出現する確率は
1-(1-10%)^22=0.9015…
より約90.2%
★4が1回出現するまで回す回数の期待値は
1/10%=10
より10回
1回以上出現するまで回すときのグラフは以下のようになります。
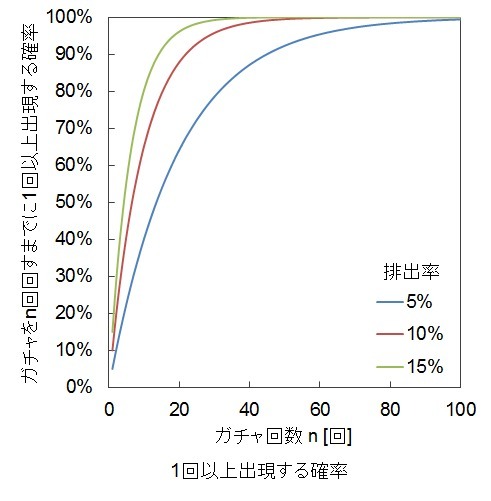
なお、★4が出現するまでにガチャを回す回数の確率は幾何分布に従います。
| ガチャを 回す回数 | ★4が1回以上出現する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 5.0 | 10.0 | 15.0 |
| 2 | 9.8 | 19.0 | 27.8 |
| 3 | 14.3 | 27.1 | 38.6 |
| 4 | 18.5 | 34.4 | 47.8 |
| 5 | 22.6 | 41.0 | 55.6 |
| 7 | 30.2 | 52.2 | 67.9 |
| 10 | 40.1 | 65.1 | 80.3 |
| 15 | 53.7 | 79.4 | 91.3 |
| 20 | 64.2 | 87.8 | 96.1 |
| 30 | 78.5 | 95.8 | 99.2 |
| 40 | 87.1 | 98.5 | 99.8 |
| 50 | 92.3 | 99.5 | 100.0 |
| 70 | 97.2 | 99.9 | 100.0 |
| 100 | 99.4 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 20.0 | 10.0 | 6.7 |
(11回刻み)
| ガチャを 回す回数 | ★4が1回以上出現する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 11 | 43.1 | 68.6 | 83.3 |
| 22 | 67.6 | 90.2 | 97.2 |
| 33 | 81.6 | 96.9 | 99.5 |
| 44 | 89.5 | 99.0 | 99.9 |
| 55 | 94.0 | 99.7 | 100.0 |
| 66 | 96.6 | 99.9 | 100.0 |
| 77 | 98.1 | 100.0 | 100.0 |
| 88 | 98.9 | 100.0 | 100.0 |
| 99 | 99.4 | 100.0 | 100.0 |
| 110 | 99.6 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 20.0 | 10.0 | 6.7 |
ある回数以上出現する確率
ガチャを何回か回すまでに★4がある回数以上出現する確率は
1-(何回か回すときに出現する★4の回数がある回数未満である確率)
です。
何回か回すときに出現する★4の回数がある回数未満である確率は、ガチャの確率分布の説明にある最下行の式を使って表せます。
したがって、★4排出率がp[%]のガチャをn回回すまでに、★4がa回以上出現する確率[%]は、Excel上で次のようになります。
=(1-BINOM.DIST(a-1,n,p%,TRUE))*100
★4がある回数出現するまでにガチャを回す回数の期待値は
(ある回数)/(★4排出率)
で表せます。
例:★4排出率が10%のガチャを回す場合
50回回すまでに★4が4回以上出現する確率はExcelに次のように入力
=(1-BINOM.DIST(4-1,50,10%,TRUE))*100
すると値が74.97…と出てくるので、約75.0%だと分かる
★4が4回以上出現するまでにガチャを回す回数の期待値は
4/10%=40
より40回
3回以上出現する場合のグラフを示します。
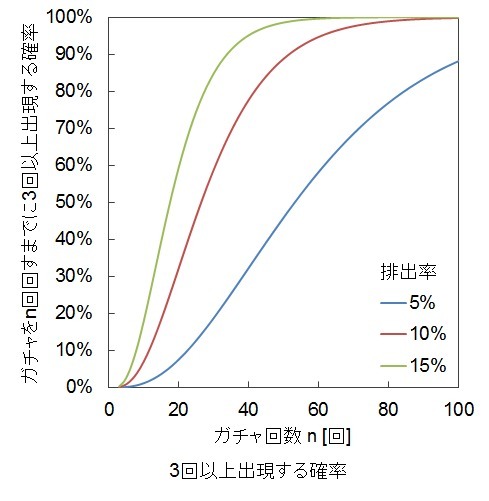
なお、★4がある回数出現するまでにガチャを回す回数の確率は負の二項分布に従うので、該当する関数を使って次のように入力しても計算結果は同じです。
=NEGBINOM.DIST(n-a,a,p%,TRUE)*100
| ガチャを 回す回数 | ★4が2回以上出現する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 2 | 0.3 | 1.0 | 2.3 |
| 5 | 2.3 | 8.1 | 16.5 |
| 10 | 8.6 | 26.4 | 45.6 |
| 15 | 17.1 | 45.1 | 68.1 |
| 20 | 26.4 | 60.8 | 82.4 |
| 30 | 44.6 | 81.6 | 95.2 |
| 40 | 60.1 | 92.0 | 98.8 |
| 50 | 72.1 | 96.6 | 99.7 |
| 60 | 80.8 | 98.6 | 99.9 |
| 70 | 87.1 | 99.5 | 100.0 |
| 80 | 91.4 | 99.8 | 100.0 |
| 90 | 94.3 | 99.9 | 100.0 |
| 100 | 96.3 | 100.0 | 100.0 |
| 150 | 99.6 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 40.0 | 20.0 | 13.3 |
| ガチャを 回す回数 | ★4が3回以上出現する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 3 | 0.0 | 0.1 | 0.3 |
| 10 | 1.2 | 7.0 | 18.0 |
| 20 | 7.5 | 32.3 | 59.5 |
| 30 | 18.8 | 58.9 | 84.9 |
| 40 | 32.3 | 77.7 | 95.1 |
| 50 | 45.9 | 88.8 | 98.6 |
| 60 | 58.3 | 94.7 | 99.6 |
| 70 | 68.6 | 97.6 | 99.9 |
| 80 | 76.9 | 98.9 | 100.0 |
| 90 | 83.4 | 99.5 | 100.0 |
| 100 | 88.2 | 99.8 | 100.0 |
| 120 | 94.2 | 100.0 | 100.0 |
| 150 | 98.2 | 100.0 | 100.0 |
| 200 | 99.8 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 60.0 | 30.0 | 20.0 |
| ガチャを 回す回数 | ★4が4回以上出現する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 4 | 0.0 | 0.0 | 0.1 |
| 10 | 0.1 | 1.3 | 5.0 |
| 20 | 1.6 | 13.3 | 35.2 |
| 30 | 6.1 | 35.3 | 67.8 |
| 40 | 13.8 | 57.7 | 87.0 |
| 50 | 24.0 | 75.0 | 95.4 |
| 60 | 35.3 | 86.3 | 98.5 |
| 70 | 46.6 | 92.9 | 99.6 |
| 80 | 57.2 | 96.5 | 99.9 |
| 90 | 66.4 | 98.3 | 100.0 |
| 100 | 74.2 | 99.2 | 100.0 |
| 120 | 85.6 | 99.8 | 100.0 |
| 150 | 94.5 | 100.0 | 100.0 |
| 200 | 99.1 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 80.0 | 40.0 | 26.7 |
1点狙いが成功する確率
ガチャの★4にいくつかの種類があるとき、特定の1種類の★4をガチャが排出する確率は
(★4排出率)/(★4の種類の数)
と表せます。ガチャをある回数回すまでに★4の1点狙いが成功する確率は、★4が1回以上出現する確率と同様にして
1-(特定の1種類の★4以外をガチャが排出する確率)^(ガチャ回数)
です。
※ただし、(特定の1種類の★4以外をガチャが排出する確率)=1-(特定の1種類の★4をガチャが排出する確率)。
★4の1点狙いが成功するまでにガチャを回す回数の期待値は、これも同様にして
1/(特定の1種類の★4をガチャが排出する確率)= (★4の種類の数)/(★4排出率)
と表せます。
例:★4排出率が10%のガチャに★4が16種類ある場合
ガチャを110回回すまでに★4の1点狙いが成功する確率は
1-(1-10%/16)^110=0.4982…
より約49.8%
★4の1点狙いが成功するまでにガチャを回す回数の期待値は
16/10%=160
より160回
特定の何種類かの★4のどれかを引き当てる確率は、(特定の1種類の★4をガチャが排出する確率)を
(★4排出率) ×(引き当てたい★4の種類の数)/(★4の種類の数)
と置き換えることで求められます。
ガチャに★4が8種類あるとき、★4の1点狙いが成功する確率、
または、★4が16種類あるとき、特定の2種類のどちらかを引き当てる確率、
または、★4が24種類あるとき、特定の3種類のどれかを引き当てる確率、
または、★4が32種類あるとき、特定の4種類のどれかを引き当てる確率
| ガチャを 回す回数 | 1点狙いが成功する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 0.625 | 1.250 | 1.875 |
| 11 | 6.7 | 12.9 | 18.8 |
| 22 | 12.9 | 24.2 | 34.1 |
| 33 | 18.7 | 34.0 | 46.5 |
| 44 | 24.1 | 42.5 | 56.5 |
| 55 | 29.2 | 49.9 | 64.7 |
| 66 | 33.9 | 56.4 | 71.3 |
| 77 | 38.3 | 62.0 | 76.7 |
| 88 | 42.4 | 66.9 | 81.1 |
| 99 | 46.2 | 71.2 | 84.6 |
| 110 | 49.8 | 74.9 | 87.5 |
| 165 | 64.5 | 87.5 | 95.6 |
| 220 | 74.8 | 93.7 | 98.4 |
| 330 | 87.4 | 98.4 | 99.8 |
| 440 | 93.7 | 99.6 | 100.0 |
| 550 | 96.8 | 99.9 | 100.0 |
| 770 | 99.2 | 100.0 | 100.0 |
| 1100 | 99.9 | 100.0 | 100.0 |
| ガチャ 回数の 期待値 | 160.0 | 80.0 | 53.3 |
ガチャに★4が16種類あるとき、★4の1点狙いが成功する確率
または、★4が32種類あるとき、特定の2種類のどちらかを引き当てる確率
| ガチャを 回す回数 | ★4の1点狙いが成功する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 0.3125 | 0.625 | 0.9375 |
| 11 | 3.4 | 6.7 | 9.8 |
| 22 | 6.7 | 12.9 | 18.7 |
| 33 | 9.8 | 18.7 | 26.7 |
| 44 | 12.9 | 24.1 | 33.9 |
| 55 | 15.8 | 29.2 | 40.4 |
| 66 | 18.7 | 33.9 | 46.3 |
| 77 | 21.4 | 38.3 | 51.6 |
| 88 | 24.1 | 42.4 | 56.3 |
| 99 | 26.6 | 46.2 | 60.6 |
| 110 | 29.1 | 49.8 | 64.5 |
| 165 | 40.3 | 64.5 | 78.9 |
| 220 | 49.8 | 74.8 | 87.4 |
| 330 | 64.4 | 87.4 | 95.5 |
| 440 | 74.8 | 93.7 | 98.4 |
| 550 | 82.1 | 96.8 | 99.4 |
| 770 | 91.0 | 99.2 | 99.9 |
| 1100 | 96.8 | 99.9 | 100.0 |
| ガチャ 回数の 期待値 | 320.0 | 160.0 | 106.7 |
ガチャに★4が24種類あるとき、★4の1点狙いが成功する確率
| ガチャを 回す回数 | ★4の1点狙いが成功する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 0.208 | 0.417 | 0.625 |
| 5 | 1.0 | 2.1 | 3.1 |
| 10 | 2.1 | 4.1 | 6.1 |
| 20 | 4.1 | 8.0 | 11.8 |
| 30 | 6.1 | 11.8 | 17.1 |
| 50 | 9.9 | 18.8 | 26.9 |
| 100 | 18.8 | 34.1 | 46.6 |
| 200 | 34.1 | 56.6 | 71.5 |
| 300 | 46.5 | 71.4 | 84.8 |
| 500 | 64.8 | 87.6 | 95.6 |
| 700 | 76.8 | 94.6 | 98.8 |
| 1000 | 87.6 | 98.5 | 99.8 |
| ガチャ 回数の 期待値 | 480.0 | 240.0 | 160.0 |
1点狙いが成功する確率がある確率となるまでにガチャを回す回数
ガチャの★4排出率をp、★4の種類の数をs、ガチャ回数をn、確率をrとしたとき、1点狙いが成功する確率がrとなるまでにガチャを回す回数は、これまでの考察から
1-(1-p/s)^n=r
をnについて解くことで得られます。
この結果は自然対数を用いて
n=ln(1-r)/ln(1-p/s)
となります。
ここで、一般にガチャが特定の1種類の★4を排出する確率p/sは十分に小さいと考えられますから、xが十分小さいときの近似式
ln(1+x)≒x
を用いることができます。したがって
n=-ln(1-r)/(p/s)
と表すことができます。
この式の中の
1/(p/s)=s/p
は★4の1点狙いが成功するまでにガチャを回す回数の期待値です。
よって、1点狙いが成功する確率がある確率となるまでにガチャを回す回数は
(★4の1点狙いが成功するまでにガチャを回す回数の期待値)×(成功確率から求められる数値)
で計算することができます。
例:★4排出率が10%、★4が16種類あるガチャを回す場合
r=95%としたとき
-ln(1-95%)≒3.0
となる。★4の1点狙いが成功するまでにガチャを回す回数の期待値は
16/10%=160
より160回。したがって、1点狙いが成功する確率が95%となるまでにガチャを回す回数のおよその数は
160×3.0=480
より480回
★4の1点狙いが成功するまでにガチャを回す回数の期待値だけガチャを回したとき、1点狙いが成功する確率は、
-ln(1-r)=1
とおいてrについて解くことで得られます。
結果は自然対数の底eを用いて
r=1-1/e=0.6321…
となります。
したがって、期待値だけ回したときは63.2%の確率で1点狙いが成功することがわかります。
近似したことによる誤差が気になるかもしれませんが、p/s=1%のときの誤差率は0.005程度です。
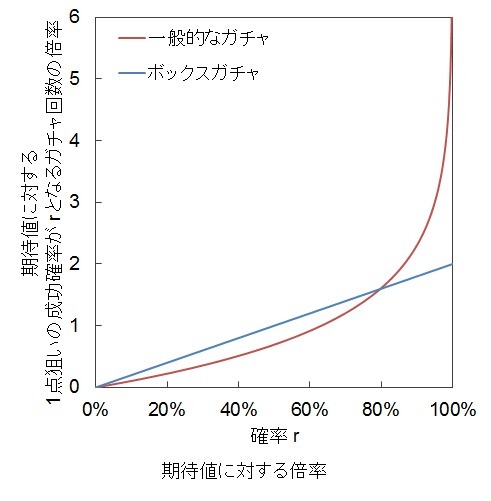
後の節での便宜上
k=-ln(1-r)
とおきます。
このkを用いると表題のガチャ回数は
s/p*k
と表せます。
下のグラフはこのkを表したものです。
比較のために現実のカプセルトイのようなガチャ(いわゆるボックスガチャ)の場合も表示しています。
| r [%] | k=-ln(1-r) |
|---|---|
| 10% | 0.11 |
| 20% | 0.22 |
| 30% | 0.36 |
| 40% | 0.51 |
| 50% | 0.69 |
| 60% | 0.92 |
| 70% | 1.2 |
| 80% | 1.6 |
| 90% | 2.3 |
| 95% | 3.0 |
| 99% | 4.6 |
| 99.5% | 5.3 |
| 99.9% | 6.9 |
| k | r=1-exp(-k) [%] |
|---|---|
| 0.1 | 9.5 |
| 0.2 | 18.1 |
| 0.3 | 25.9 |
| 0.4 | 33.0 |
| 0.5 | 39.3 |
| 0.6 | 45.1 |
| 0.7 | 50.3 |
| 0.8 | 55.1 |
| 0.9 | 59.3 |
| 1 | 63.2 |
| 1.1 | 66.7 |
| 1.2 | 69.9 |
| 1.3 | 72.7 |
| 1.4 | 75.3 |
| 1.5 | 77.7 |
| 2 | 86.5 |
| 3 | 95.0 |
| 4 | 98.2 |
| 5 | 99.33 |
| 10 | 99.9955 |
ある確率でやめる場合の期待値
現実には無限にガチャを回すことはできませんから、1点狙いが成功しなくても途中でガチャを回すのをやめる場合の期待値を求めてみます。
★4の1点狙いが成功するか、1点狙いが成功する確率がある確率となるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値は
(★4の1点狙いが成功するまでにガチャを回す回数の期待値)×(ある確率)
です。
前の節で用いられる文字で表すと
s/p*r
となります。
例:★4排出率が10%、★4が16種類あるガチャを回す場合
★4の1点狙いが成功するか、1点狙いが成功する確率が50%となるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値は
16/10%×50%=80
より80回
ガチャに★4が8種類あるとき、★4の1点狙いが成功するか、1点狙いが成功する確率がrとなるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値
| r [%] | 期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 10 | 16 | 8 | 5 |
| 20 | 32 | 16 | 11 |
| 30 | 48 | 24 | 16 |
| 40 | 64 | 32 | 21 |
| 50 | 80 | 40 | 27 |
| 60 | 96 | 48 | 32 |
| 70 | 112 | 56 | 37 |
| 80 | 128 | 64 | 43 |
| 90 | 144 | 72 | 48 |
| 95 | 152 | 76 | 51 |
| 99 | 158 | 79 | 53 |
| 99.5 | 159 | 80 | 53 |
| 99.9 | 160 | 80 | 53 |
ガチャに★4が16種類あるとき、★4の1点狙いが成功するか、1点狙いが成功する確率がrとなるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値
| r [%] | 期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 10 | 32 | 16 | 11 |
| 20 | 64 | 32 | 21 |
| 30 | 96 | 48 | 32 |
| 40 | 128 | 64 | 43 |
| 50 | 160 | 80 | 53 |
| 60 | 192 | 96 | 64 |
| 70 | 224 | 112 | 75 |
| 80 | 256 | 128 | 85 |
| 90 | 288 | 144 | 96 |
| 95 | 304 | 152 | 101 |
| 99 | 317 | 158 | 106 |
| 99.5 | 318 | 159 | 106 |
| 99.9 | 320 | 160 | 107 |
あるガチャ回数でやめる場合の期待値
★4排出率をp、★4の種類の数をsとします。
4の1点狙いが成功するか、ガチャ回数がnに達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値は
s/p*(1-(1-p/s)^n)
です。
例:★4排出率が10%、★4が16種類あるガチャを回す場合
★4の1点狙いが成功するか、ガチャ回数が110回に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値は
16/10%*(1-(1-10%/16)^110)=79.72…
より約80回
これまでの考察を用いて
s/p*r=s/p*(1-exp(-N*p/s))
としても計算できます。
ガチャに★4が8種類あるとき、★4の1点狙いが成功するか、ガチャ回数がn=8k/pに達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値
| k | 期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0.1 | 15 | 8 | 5 |
| 0.2 | 29 | 15 | 10 |
| 0.3 | 41 | 21 | 14 |
| 0.4 | 53 | 26 | 18 |
| 0.5 | 63 | 31 | 21 |
| 0.6 | 72 | 36 | 24 |
| 0.7 | 81 | 40 | 27 |
| 0.8 | 88 | 44 | 29 |
| 0.9 | 95 | 47 | 32 |
| 1 | 101 | 51 | 34 |
| 1.1 | 107 | 53 | 36 |
| 1.2 | 112 | 56 | 37 |
| 1.3 | 116 | 58 | 39 |
| 1.4 | 121 | 60 | 40 |
| 1.5 | 124 | 62 | 41 |
| 2 | 138 | 69 | 46 |
| 3 | 152 | 76 | 51 |
| 4 | 157 | 79 | 52 |
| 5 | 159 | 79 | 53 |
| 10 | 160 | 80 | 53 |
ガチャに★4が16種類あるとき、★4の1点狙いが成功するか、ガチャ回数がn=16k/pに達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値
| k | 期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 0.1 | 30 | 15 | 10 |
| 0.2 | 58 | 29 | 19 |
| 0.3 | 83 | 41 | 28 |
| 0.4 | 105 | 53 | 35 |
| 0.5 | 126 | 63 | 42 |
| 0.6 | 144 | 72 | 48 |
| 0.7 | 161 | 81 | 54 |
| 0.8 | 176 | 88 | 59 |
| 0.9 | 190 | 95 | 63 |
| 1 | 202 | 101 | 67 |
| 1.1 | 213 | 107 | 71 |
| 1.2 | 224 | 112 | 75 |
| 1.3 | 233 | 116 | 78 |
| 1.4 | 241 | 121 | 80 |
| 1.5 | 249 | 124 | 83 |
| 2 | 277 | 138 | 92 |
| 3 | 304 | 152 | 101 |
| 4 | 314 | 157 | 105 |
| 5 | 318 | 159 | 106 |
| 10 | 320 | 160 | 107 |
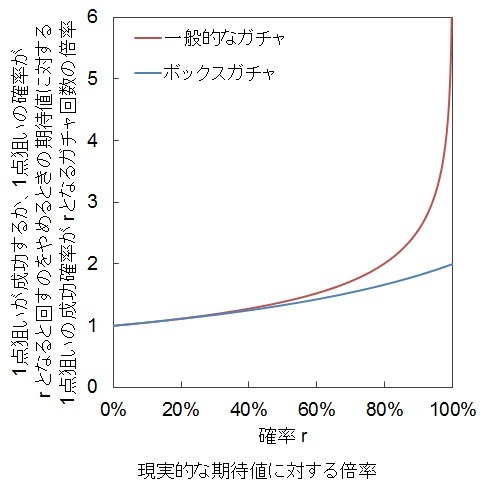
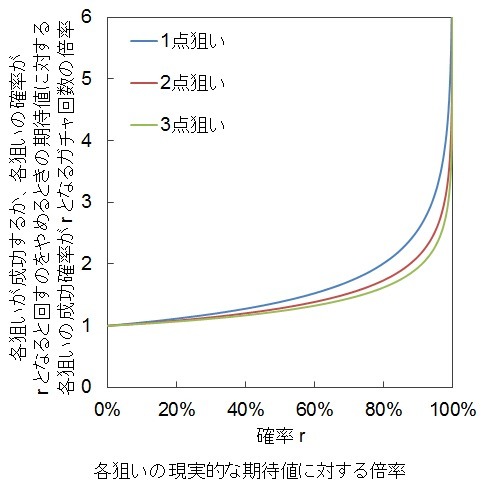
現実的な期待値に対する倍率
最大でN回ガチャを回せるとして、r=1-exp(-N*p/s)の確率で1点狙いを成功させる場合の様子を調べます。
(1点狙いが成功する確率がr以上となるまでにガチャを回す回数)
を
(★4の1点狙いが成功するか、1点狙いが成功する確率がr以上となるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値のおよその数)
で割ってみます。
N/(s/p*r)
=(s/p*k)/(s/p*r)
=k/r
=-ln(1-r)/r
rが0%に近いときはこの倍率は1に近い値になります。
逆にrが100%に近づくとこの倍率は無限大に発散します。
これはrが小さいときは最大のガチャ回数が現実的な期待値に近いが、rが大きくしていくと最大のガチャ回数が現実的な期待値に対して爆発的に増加する、ということを意味しています。
下のグラフはこの倍率を表したものです。
比較のためにボックスガチャの場合も表示しています。
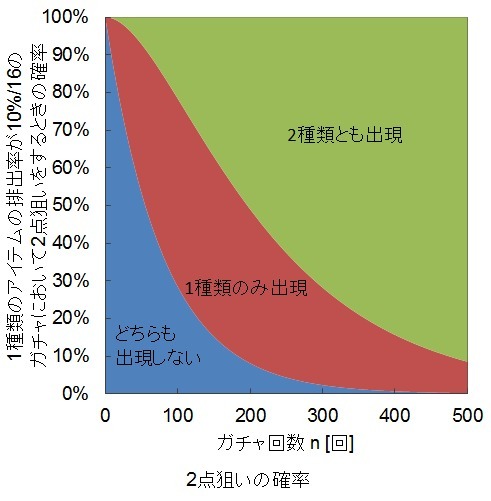
2点狙いが成功する確率
いくつかある★4のうち、2種類を狙って両方とも引き当てる確率です。
★4排出率をp、★4の種類の数をsとします。
ガチャをn回回すまでに2点狙いが成功する確率は
1-2*(1-p/s)^n+(1-2*p/s)^n
です。
ガチャをn回回すまでに狙っている2種類のどちらも出現しない確率は
(1-2*p/s)^n
です。
★4排出率が10%、★4が16種類あるガチャを回した場合を下の図に示します。
2点狙いが成功するまでにガチャを回す回数の期待値は
(★4の種類の数)/(★4排出率)×1.5
です。
なお、3点狙いが成功するまでにガチャを回す回数の期待値は
(★4の種類の数)/(★4排出率)×11/6
です。
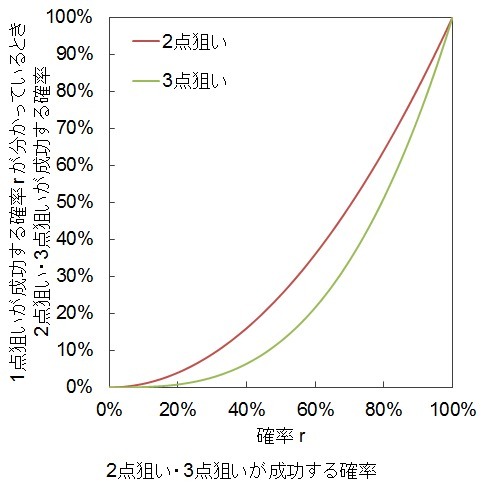
1点狙いが成功する確率が分かっているときの2点狙い・3点狙いが成功する確率
ある回数ガチャを回すまでに1点狙いが成功する確率が分かっているとき、この回数回すまでに2点狙いが成功する確率のおよその値は
(ある回数ガチャを回すまでに1点狙いが成功する確率)^2
です。
例:ある回数ガチャを回すまでに1点狙いが成功する確率が50%の場合
この回数回すまでに2点狙いが成功する確率のおよその値は
50%^2=0.25
より25%
ある回数ガチャを回すまでに1点狙いが成功する確率が分かっているとき、この回数回すまでに3点狙いが成功する確率のおよその値は
(ある回数ガチャを回すまでに1点狙いが成功する確率)^3
です。
例:ある回数ガチャを回すまでに1点狙いが成功する確率が50%の場合
この回数回すまでに3点狙いが成功する確率のおよその値は
50%^3=0.125
より12.5%
図はこの関数をプロットしたものです。
狙いが成功する確率がある確率となるまでにガチャを回す回数
2点狙いが成功する確率がrとなるまでにガチャを回す回数は
s/p*(-ln(1-√r))
です。
3点狙いが成功する確率がrとなるまでにガチャを回す回数は
s/p*(-ln(1-r^(1/3)))
です。
この回数を
(1点狙いが成功するまでにガチャを回す回数の期待値)
で割ったものが次の図です。
この回数を
(各狙いが成功するまでにガチャを回す回数の期待値)
で割ったものが次の図です。
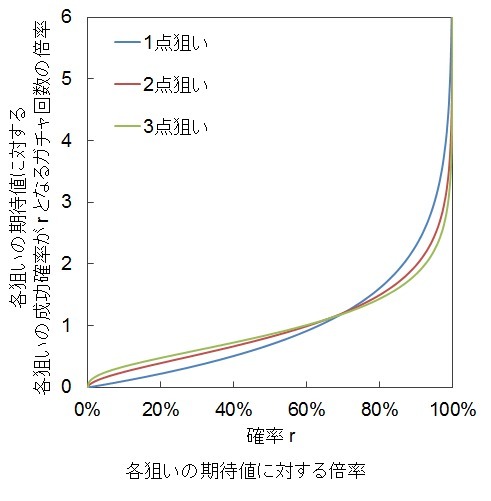
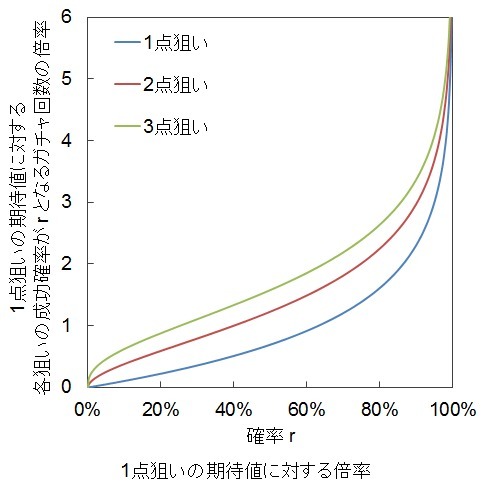
各狙いの現実的な期待値に対する倍率
(狙いが成功する確率がrとなるまでにガチャを回す回数)
を
(狙いが成功するか、狙いが成功する確率がrとなるガチャ回数に達するとガチャを回すのをやめるとき、ガチャを回す回数の期待値のおよその数)
で割ってみたときのグラフを下に示します。
狙いが成功する確率からガチャ回数を暗算で導く方法
次のことを覚えておくと1点狙いが成功する確率rから必要なガチャ回数を暗算で導くことができます。
1. (1点狙いが成功するまでにガチャを回す回数の期待値)
=(★4の種類の数)÷(★4排出率)
2. 1点狙いが成功する確率 r に対応する k の値
3. (1点狙いが成功する確率がrとなるガチャ回数)
=(★4の種類の数)÷(★4排出率)×k
また、次のことを覚えておくと1点狙いが成功する確率rから各狙いが成功する確率を導くことができます。
4. (2点狙いが成功する確率) = rの2乗
5. (3点狙いが成功する確率) = rの3乗
rに対応するkの値はこの欄に載っていますが、覚えやすいよう表にまとめました。
| 1点狙いが 成功する確率 r | 期待値に対する 倍率 ×k | 2点狙いが 成功する確率 rの2乗 | 3点狙いが 成功する確率 rの3乗 |
|---|---|---|---|
| 10% | ×0.1 | 1% | 0.1% |
| 20% | ×0.2 | 4% | 0.8% |
| 30% | ×0.35 | 9% | 3% |
| 40% | ×0.5 | 15% | 6% |
| 50% | ×0.7 | 25% | 12.5% |
| 63% | ×1 | 40% | 25% |
| 70% | ×1.2 | 50% | 35% |
| 80% | ×1.5 | 65% | 50% |
| 90% | ×2.3 | 80% | 70% |
| 95% | ×3 | 90% | 85% |
| 99% | ×4.5 | 98% | 97% |
太字のところは特に覚えておくとよいでしょう。
さらに、t種類のうちどれでもよいから狙っている場合は次のようにtで割ることで求められます。
6. (t種類のうちどれでもよいから出現する確率がrとなるガチャ回数)
=(★4の種類の数)÷(★4排出率)×k ÷t
例:★4排出率が10%、★4が16種類あるガチャを回す場合
(★4の種類の数)÷(★4排出率)=160回
r=40%のときk=0.5
160回×0.5=80回
よって1点狙いが成功する確率が40%となるガチャ回数は80回
例:★4排出率が10%、★4が16種類あるガチャを回す場合
(★4の種類の数)÷(★4排出率)=160回
r=80%のときk=1.5
160回×1.5=240回
80%^2≒65%
よって2点狙いが成功する確率が65%となるガチャ回数は240回
例:★4排出率が10%、★4が16種類あるガチャを回す場合
(★4の種類の数)÷(★4排出率)=160回
r=95%のときk=3
160回×3=480回
480回÷2=240回
よって2種類のうちどちらでもよいから出現する確率が95%となるガチャ回数は240回
白猫プロジェクトでは、限定キャラガチャにおける★4の種類の数が通常キャラガチャの★4の種類の数の半分となっていることがほとんどです。
このときは、通常キャラガチャにおけるガチャ回数の結果から限定キャラガチャにおけるガチャ回数を次のように2で割ることで求められます。
7. (限定キャラガチャにおけるガチャ回数)
=(通常キャラガチャにおけるガチャ回数) ÷2
例:★4排出率が10%、★4が8種類あるガチャを回す場合
前の例の結果より、16種類あるガチャにおいて1点狙いが成功する確率が40%となるガチャ回数は80回
80回÷2=40回
よって1点狙いが成功する確率が40%となるガチャ回数は40回
もちろん、白猫プロジェクト以外のガチャにおいても期待値から同じように暗算でガチャ回数を導くことができます。
白猫プロジェクトにおける(★4の種類の数)÷(★4排出率)の式は一般的には
(1点狙いが成功するまでにガチャを回す回数の期待値)
=1/(そのアイテムの排出率)
となります。
その他の確率
その他の確率のページへ
- リセマラの確率
- 被る確率
- 被りがある確率
- ★4をそろえるまでのガチャ回数の期待値
- キャラクターにモチーフ武器を持たせるまでのガチャ回数の期待値
ガチャ確率の計算式一覧
ガチャ確率の計算式一覧のページへ
-
-

-
冒険者さん
-
-
-

-
冒険者さん
12168年まえ ID:blbxq3it半年で924連して☆4と5合わせて18
引いたのはイベント☆5ありのみなので11%のはずが1.9%ほど;
ひどすぎるわ
-
-
-

-
冒険者さん
12158年まえ ID:je3v0nva2年ちょっとやってる
虹ルーンを一切使っていないので確率計算ができる
☆4確率 9.1%前後
この確率を下回ると当たりが増え、上回ると爆死が増える
サンプル数1だがご参考
-
-
-

-
冒険者さん
12149年まえ ID:h9jdj5ls初期からやってて今まで引いた回数2445回
最初の確率低かった頃も入ってるからあれだけど
☆2 50.51% (1235)
☆3 39.80% (973)
☆4 9.69% (237)
↑の8.4~11.1%って区間的にも
平均は☆4率9.75%くらいじゃないかと予想
-
-
-

-
冒険者さん
12139年まえ ID:s7s633b1体感では星4が出る確率10パーセントもないなぁ…
確率以上に不運はどうしようもないか
-
-
-

-
冒険者さん
12129年まえ ID:cuvybb3w66連☆4なしで77連目に☆4が2体メイリンとモニカ
メイリン以外の3キャラならどれでも良かったのに物欲センサーつらい
-
-
-

-
冒険者さん
12119年まえ ID:g8ipv9iz入替キャラ0.5%、0.25%、0.1%の試算もみたいな~
頭のいい人いないかな~
-
-
-

-
冒険者さん
12109年まえ ID:jaia6q7mキャラ11連5回やって星4無しって…なけなしのジュエルなのに…泣きそう…
-
-
-

-
冒険者さん
-
-
-

-
冒険者さん
12089年まえ ID:qk74qdsq「★4排出率の推定」のページは読まれましたか? キャラガチャ合算2011回の検証において、★4排出率の推定値は9.8%、また★4排出率の信頼度95%の信頼区間は8.4%〜11.1%と統計学的に算出されています。
個人的な体感なんていう不確かなもので確率に口を挟まないでいただきたいのです。★4排出率が10%に設定されていて体感7〜8%だなんてことはザラにあることです。というかそもそも体感で7〜8%なら10%がおかしいとは思わないはず。確率を全く理解できていない方とお見受けします
-


















































