その他の確率
ガチャの確率に戻る
リセマラの確率
リセマラをするときに★4を1個以上入手する確率は
1-(リセマラ1回に★4が1回も出現しない確率)^(リセマラをする回数)
で与えられます。
※ただし、(リセマラ1回に★4が1回も出現しない確率)=(1-(★4排出率))^(リセマラ1回にガチャを回す回数)。
リセマラで★4を1個以上入手するまでにリセマラをする回数の期待値は、これも同様にして
1÷(リセマラ1回に★4が1回以上出現する確率)
です。
例:★4排出率が10%のガチャをリセマラ1回につき7回回す場合
リセマラ1回に★4が1回も出現しない確率は
(1-10%)^7=0.4782…
より約47.8%
リセマラ3回目までに★4を1個以上入手する確率は
1-0.478^3=0.8907…
より89.1%
リセマラをする回数の期待値は
1÷(1-0.4782)=1.916…
より約1.9回
結局、リセマラをするときに★4を1個以上入手する確率は、
1-(1-(★4排出率))^*1
と表せることになります。これは、*2回ガチャを回すまでに★4が1回以上出現する確率と同じです。
リセマラで★4の1点狙いが成功する確率は、上記※の★4排出率を
(★4排出率)÷(★4の種類の数)
に置き換えて計算することで得られます。
リセマラについての詳細はこちら
リセマラ1回に7回ガチャを回すとき、★4を1個以上入手する確率
| リセマラ の回数 | ★4を1個以上入手する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 30.2 | 52.2 | 67.9 |
| 2 | 51.2 | 77.1 | 89.7 |
| 3 | 65.9 | 89.1 | 96.7 |
| 4 | 76.2 | 94.8 | 98.9 |
| 5 | 83.4 | 97.5 | 99.7 |
| 6 | 88.4 | 98.8 | 99.9 |
| 7 | 91.9 | 99.4 | 100.0 |
| 8 | 94.3 | 99.7 | 100.0 |
| 9 | 96.1 | 99.9 | 100.0 |
| 10 | 97.2 | 99.9 | 100.0 |
| 12 | 98.7 | 100.0 | 100.0 |
| 15 | 99.5 | 100.0 | 100.0 |
| 20 | 99.9 | 100.0 | 100.0 |
| リセマラ 回数の 期待値 | 3.3 | 1.9 | 1.5 |
リセマラ1回に★4が8種類あるガチャを7回回すとき、★4の1点狙いが成功する確率、
または、★4が16種類あるガチャを同様に回すとき、特定の2種類のどちらかを引き当てる確率、
または、★4が24種類あるガチャを同様に回すとき、特定の3種類のどれかを引き当てる確率、
または、★4が32種類あるガチャを同様に回すとき、特定の4種類のどれかを引き当てる確率
| リセマラ の回数 | ★4の1点狙いが成功する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 4.3 | 8.4 | 12.4 |
| 2 | 8.4 | 16.1 | 23.3 |
| 3 | 12.3 | 23.2 | 32.8 |
| 4 | 16.1 | 29.7 | 41.1 |
| 5 | 19.7 | 35.6 | 48.4 |
| 7 | 26.5 | 46.0 | 60.4 |
| 10 | 35.5 | 58.5 | 73.4 |
| 15 | 48.2 | 73.3 | 86.3 |
| 20 | 58.4 | 82.8 | 92.9 |
| 30 | 73.2 | 92.9 | 98.1 |
| 40 | 82.7 | 97.0 | 99.5 |
| 50 | 88.9 | 98.8 | 99.9 |
| 70 | 95.4 | 99.8 | 100.0 |
| 100 | 98.8 | 100.0 | 100.0 |
| リセマラ 回数の 期待値 | 23.3 | 11.9 | 8.1 |
リセマラ1回に★4が16種類あるガチャを7回回すとき、★4の1点狙いが成功する確率、
または、★4が32種類あるガチャを同様に回すとき、特定の2種類のどれかを引き当てる確率
| リセマラ の回数 | ★4の1点狙いが成功する確率[%] | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 2.2 | 4.3 | 6.4 |
| 2 | 4.3 | 8.4 | 12.4 |
| 3 | 6.4 | 12.3 | 17.9 |
| 4 | 8.4 | 16.1 | 23.2 |
| 5 | 10.4 | 19.7 | 28.1 |
| 7 | 14.2 | 26.5 | 37.0 |
| 10 | 19.7 | 35.5 | 48.3 |
| 15 | 28.0 | 48.2 | 62.8 |
| 20 | 35.5 | 58.4 | 73.3 |
| 30 | 48.2 | 73.2 | 86.2 |
| 40 | 58.4 | 82.7 | 92.8 |
| 50 | 66.6 | 88.9 | 96.3 |
| 70 | 78.4 | 95.4 | 99.0 |
| 100 | 88.8 | 98.8 | 99.9 |
| 150 | 96.3 | 99.9 | 100.0 |
| 200 | 98.7 | 100.0 | 100.0 |
| リセマラ 回数の 期待値 | 46.1 | 23.3 | 15.7 |
被る確率
中身が同じガチャを回す場合を考えます。
ガチャから出現する★4をすでに何種類か持っているとき、次に出現する★4が持っている★4と被る確率は
(持っている★4の種類の数)÷(ガチャの★4の種類の数)
で表せます。
例:ガチャから出現する★4を2種類持っている場合
次に出現する★4が被る確率は
2÷16=0.125…
より約12.5%
| 持っている ★4の 種類の数 | 次に出現する★4が 被る確率[%] | ||
|---|---|---|---|
| ガチャの★4の種類の数 | |||
| 8 | 16 | 24 | |
| 0 | 0 | 0 | 0 |
| 1 | 12.5 | 6.3 | 4.2 |
| 2 | 25.0 | 12.5 | 8.3 |
| 3 | 37.5 | 18.8 | 12.5 |
| 4 | 50.0 | 25.0 | 16.7 |
| 5 | 62.5 | 31.3 | 20.8 |
| 6 | 75.0 | 37.5 | 25.0 |
| 7 | 87.5 | 43.8 | 29.2 |
| 8 | 100 | 50.0 | 33.3 |
| 9 | - | 56.3 | 37.5 |
| 10 | - | 62.5 | 41.7 |
| 11 | - | 68.8 | 45.8 |
| 12 | - | 75.0 | 50.0 |
| 13 | - | 81.3 | 54.2 |
| 14 | - | 87.5 | 58.3 |
| 15 | - | 93.8 | 62.5 |
| 16 | - | 100 | 66.7 |
| 17 | - | - | 70.8 |
| 18 | - | - | 75.0 |
| 19 | - | - | 79.2 |
| 20 | - | - | 83.3 |
| 21 | - | - | 87.5 |
| 22 | - | - | 91.7 |
| 23 | - | - | 95.8 |
| 24 | - | - | 100 |
被りがある確率
中身が同じガチャを回す場合を考えます。
★4が何回か出現したとき、被りがある確率は
1-(被りが1つもない確率)
で表せます。
被りが1つもない確率は、
(すでにいくつか種類を選んだとき、次に選ぶ★4が被らない確率)
を出現回数だけ掛け算していくことで得られます。
例:★4が8種類あるガチャを何回か回して★4が3回出現した場合
何も★4の種類を選んでいないとき、被らない8種類を選ぶ確率は
8/8
★4を1種類選んだとき、被らない7種類を選ぶ確率は
7/8
★4を2種類選んだとき、被らない6種類を選ぶ確率は
6/8
よって、被りが1つもない確率は
8/8×7/8×6/8=0.6562…
となるから、被りがある確率は
1-0.6562=0.3438
より約34.4%
被りがある確率のグラフを下の図に示します。
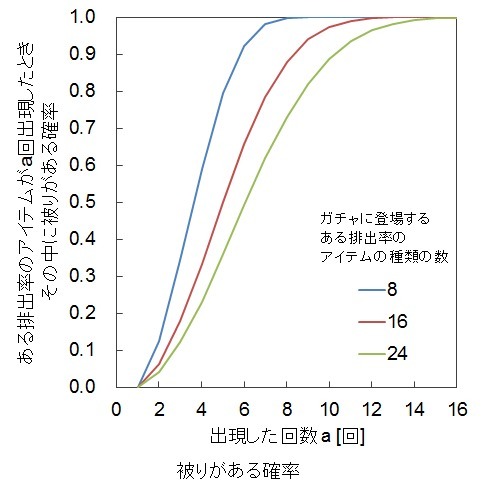
★4に被りがある確率
| 出現した ★4の回数 | ★4に 被りがある 確率[%] | ||
|---|---|---|---|
| ガチャの★4の種類の数 | |||
| 8 | 16 | 24 | |
| 1 | 0.0 | 0.0 | 0.0 |
| 2 | 12.5 | 6.3 | 4.2 |
| 3 | 34.4 | 18.0 | 12.2 |
| 4 | 59.0 | 33.3 | 23.1 |
| 5 | 79.5 | 50.0 | 35.9 |
| 6 | 92.3 | 65.6 | 49.3 |
| 7 | 98.1 | 78.5 | 62.0 |
| 8 | 99.8 | 87.9 | 73.1 |
| 9 | 100 | 94.0 | 82.0 |
| 10 | 100 | 97.4 | 88.8 |
| 11 | 100 | 99.0 | 93.5 |
| 12 | 100 | 99.7 | 96.5 |
| 13 | 100 | 99.9 | 98.2 |
| 14 | 100 | 100.0 | 99.2 |
| 15 | 100 | 100.0 | 99.7 |
| 16 | 100 | 100.0 | 99.9 |
| 17~24 | 100 | 100 | 100.0 |
| 25以上 | 100 | 100 | 100 |
★4をそろえるまでのガチャ回数の期待値
中身が同じガチャを回す場合を考えます。
どれでもよいからそろえる場合
どれでもよいから★4をそろえるまでにガチャを回す回数の期待値は
(すでにいくつかそろっているとき、まだそろっていない★4が出現するまでにガチャを回す回数の期待値)
を足し算していくことで得られます。
例:★4排出率が10%(=1/10)、★4が8種類あるガチャを回して、どれでもよいから★4を3種類そろえる場合
★4の特定の1種類が出現する確率は
1/10÷8=1/80
何も持っていないとき、★4のうちのどれかが出現するまでにガチャを回す回数の期待値は、★4が1回出現するまでにガチャを回す回数の期待値を参考にして
1÷(1/80×8)=80/8
★4が1種類そろっているとき、まだそろっていない6種類の★4のうちのどれかが出現するまでにガチャを回す回数の期待値は
1÷(1/80×7)=80/7
★4が2種類そろっているとき、まだそろっていない5種類の★4のうちのどれかが出現するまでにガチャを回す回数の期待値は
1÷(1/70×5)=80/6
したがって、どれでもよいから★4を3種類そろえるまでにガチャを回す回数の期待値は
80/8+80/7+80/6=34.76…
より、約35回
特定のをそろえる場合
特定の★4をそろえるまでにガチャを回す回数の期待値は
(すでにいくつかそろっているとき、まだそろっていない特定の★4が出現するまでにガチャを回す回数の期待値)
を足し算していくことで得られます。
例:★4排出率が10%(=1/10)、★4が8種類あるガチャを回して、特定の★4を3種類そろえる場合を考えます。
★4の特定の1種類が出現する確率は
1/10÷8=1/80
何も持っていないとき、特定の3種類の★4のうちのどれかが出現するまでにガチャを回す回数の期待値は、★4が1回出現するまでにガチャを回す回数の期待値を参考にして
1÷(1/80×3)=80/3
特定の★4のうち1種類そろっているとき、まだそろっていない特定の2種類の★4のうちのどちらかが出現するまでにガチャを回す回数の期待値は
1÷(1/80×2)=80/2
特定の★4のうち2種類そろっているとき、まだそろっていない特定の1種類が出現するまでにガチャを回す回数の期待値は
1÷(1/80×1)=80/1
したがって、特定の★4を3種類そろえるまでにガチャを回す回数の期待値は
80/3+80/2+80/1=146.66…
より、約147回
下の図はそろえる場合のガチャ回数を1点狙いが成功する確率で割ったものです。
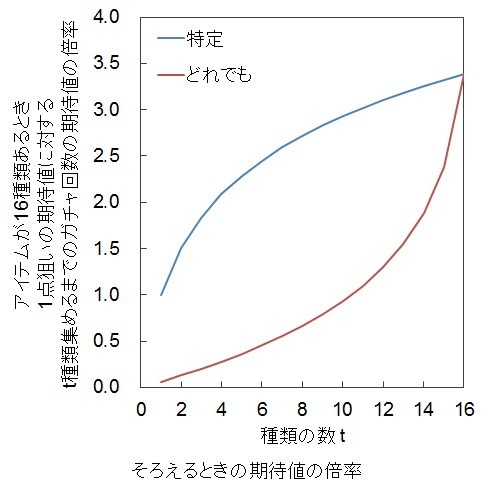
※各表の1番下の行は、★4をコンプリートするまでにガチャを回す回数の期待値です。
ガチャに★4が8種類あるとき、どれでもよいからそろえる場合
※★4が16または24または32種類あるガチャを回して、どれでもよいから★4の職業をそろえる場合もこの期待値です。
| そろえる ★4の 種類の数 =b | どれでもよいから ★4をb種類そろえるまでに ガチャを回す回数の期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 20 | 10 | 7 |
| 2 | 43 | 21 | 14 |
| 3 | 70 | 35 | 23 |
| 4 | 102 | 51 | 34 |
| 5 | 142 | 71 | 47 |
| 6 | 195 | 97 | 65 |
| 7 | 275 | 137 | 92 |
| 8 | 435 | 217 | 145 |
ガチャに★4が8種類あるとき、特定のをそろえる場合
※★4が16または24または32種類あるガチャを回して、特定の★4の職業をそろえる場合もこの期待値です。
| そろえる ★4の 種類の数 =b | 特定の★4をb種類そろえるまでに ガチャを回す回数の期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 160 | 80 | 53 |
| 2 | 240 | 120 | 80 |
| 3 | 293 | 147 | 98 |
| 4 | 333 | 167 | 111 |
| 5 | 365 | 183 | 122 |
| 6 | 392 | 196 | 131 |
| 7 | 415 | 207 | 138 |
| 8 | 435 | 217 | 145 |
ガチャに★4が16種類あるとき、どれでもよいからをそろえる場合
| そろえる ★4の 種類の数 =b | どれでもよいから ★4をb種類そろえるまでに ガチャを回す回数の期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 20 | 10 | 7 |
| 2 | 41 | 21 | 14 |
| 3 | 64 | 32 | 21 |
| 4 | 89 | 44 | 30 |
| 5 | 115 | 58 | 38 |
| 6 | 145 | 72 | 48 |
| 7 | 177 | 88 | 59 |
| 8 | 212 | 106 | 71 |
| 9 | 252 | 126 | 84 |
| 10 | 298 | 149 | 99 |
| 11 | 351 | 176 | 117 |
| 12 | 415 | 208 | 138 |
| 13 | 495 | 248 | 165 |
| 14 | 602 | 301 | 201 |
| 15 | 762 | 381 | 254 |
| 16 | 1082 | 541 | 361 |
ガチャに★4が16種類あるとき、特定のをそろえる場合
| そろえる ★4の 種類の数 =b | 特定の★4をb種類そろえるまでに ガチャを回す回数の期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 320 | 160 | 107 |
| 2 | 480 | 240 | 160 |
| 3 | 587 | 293 | 196 |
| 4 | 667 | 333 | 222 |
| 5 | 731 | 365 | 244 |
| 6 | 784 | 392 | 261 |
| 7 | 830 | 415 | 277 |
| 8 | 870 | 435 | 290 |
| 9 | 905 | 453 | 302 |
| 10 | 937 | 469 | 312 |
| 11 | 966 | 483 | 322 |
| 12 | 993 | 497 | 331 |
| 13 | 1018 | 509 | 339 |
| 14 | 1040 | 520 | 347 |
| 15 | 1062 | 531 | 354 |
| 16 | 1082 | 541 | 361 |
キャラクターにモチーフ武器を持たせるまでのガチャ回数の期待値
持っているキャラクターのモチーフ武器が武器ガチャに登場する場合を考えます。
武器ガチャを回して持っているキャラクターのモチーフ武器を1個入手するまでガチャを回す回数の期待値は
(武器ガチャの★4の種類の数)÷(★4排出率)÷(持っているキャラクターの種類の数)
です。
例:持っているキャラクターの種類が4種類あるとき、★4排出率が10%で★4が24種類ある武器ガチャを回す場合
計算式は
24÷10%÷4=60
より求める期待値は60回
キャラクターと武器を読み替えても、同様に成り立ちます。
★4が24種類ある武器ガチャを回す場合
| 持っている キャラクター の種類の数 | 持っているキャラクターの モチーフ武器を1個入手するまでに ガチャを回す回数の期待値 | ||
|---|---|---|---|
| ★4排出率[%] | |||
| 5 | 10 | 15 | |
| 1 | 480 | 240 | 160 |
| 2 | 240 | 120 | 80 |
| 3 | 160 | 80 | 53 |
| 4 | 120 | 60 | 40 |
| 5 | 96 | 48 | 32 |
| 6 | 80 | 40 | 27 |
| 7 | 69 | 34 | 23 |
| 8 | 60 | 30 | 20 |
| 9 | 53 | 27 | 18 |
| 10 | 48 | 24 | 16 |
| 11 | 44 | 22 | 15 |
| 12 | 40 | 20 | 13 |
| 13 | 37 | 18 | 12 |
| 14 | 34 | 17 | 11 |
| 15 | 32 | 16 | 11 |
| 16 | 30 | 15 | 10 |
















































